题目内容
1.已知定义在R上的函数f(x)对任意的实数x,都有f(x-2)=-f(x),且当x∈[-2,0],y∈R时,f(x+y)+f(x)=2x3-4(x+y)2,则y=f(x)在x=5处的切线方程为9x-y-26=0.分析 将x换为x+2,可得f(x+4)=f(x),即有f(x)=x3-2(x+4)2,x∈[-2,0],即有f(5)=f(1)=-f(-1)=19,再由两边对x求导,可得f′(5)=f′(1)=-f′(-1)=9,再由直线的点斜式方程可得所求切线的方程.
解答 解:f(x-2)=-f(x),可得
f(x)=-f(x+2),即有f(x+4)=f(x),
令y=4,可得f(x+4)+f(x)=2x3-4(x+4)2,
即有f(x)=x3-2(x+4)2,x∈[-2,0],
即有f(5)=f(1)=-f(-1)=-(-1-2×9)=19,
由f(x+4)=f(x),求导可得f′(x+4)=f′(x),
f(x)=x3-2(x+4)2,x∈[-2,0],可得
f′(x)=3x2-4(x+4),
即有f′(5)=f′(1),
f(x-2)=-f(x),两边求导,可得
f′(x-2)=-f′(x),
则f′(1)=-f′(-1)=-(3-4×3)=9,
即有y=f(x)在x=5处的切线斜率为9,
则y=f(x)在x=5处的切线方程为y-19=9(x-5),即为9x-y-26=0.
故答案为:9x-y-26=0.
点评 本题考查函数的周期性及运用,考查导数的运用:求切线的方程,考查运算能力,属于中档题.

练习册系列答案
相关题目
9.如果$\sqrt{x+\sqrt{2}}$+|y-1|=0,则|$\frac{1}{x+y}$|=( )
| A. | 1-$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | -$\sqrt{2}$-1 |
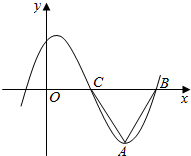 已知向量$\overrightarrow{a}$=(2cos$\frac{ωx}{2}$,$\sqrt{3}$),$\overrightarrow{b}$=(3cos$\frac{ωx}{2}$,sinωx),ω>0,设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-3的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且△ABC为等边三角形,其高为2$\sqrt{3}$.
已知向量$\overrightarrow{a}$=(2cos$\frac{ωx}{2}$,$\sqrt{3}$),$\overrightarrow{b}$=(3cos$\frac{ωx}{2}$,sinωx),ω>0,设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-3的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且△ABC为等边三角形,其高为2$\sqrt{3}$.