题目内容
13.在区间[0,1]中随机取出两个数,则两数之和不小于$\frac{4}{5}$的概率是( )| A. | $\frac{8}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{18}{25}$ | D. | $\frac{17}{25}$ |
分析 根据几何概型的计算公式,求出满足条件的面积比即可.
解答 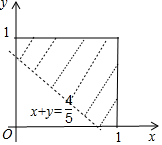 解:设取出的两个数为x、y;
解:设取出的两个数为x、y;
则有0≤x≤1,0≤y≤1,
其表示的区域为纵横坐标都在[0,1]之间的正方形区域,
其面积为1,
而x+y>$\frac{4}{5}$表示的区域为直线x+y=$\frac{4}{5}$上方,
且在0≤x≤1,0≤y≤1表示区域内部的部分,如图所示,
易得其面积为1-$\frac{1}{2}$×${(\frac{4}{5})}^{2}$=$\frac{17}{25}$;
则两数之和不小于$\frac{4}{5}$的概率是$\frac{17}{25}$.
故选:D.
点评 本题考查了几何概型的概率计算问题,解题的关键是用平面区域表示出面积关系,是基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
1.sin(-690°)的值为( )
| A. | $({\frac{{\sqrt{3}}}{2}})$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
18.已知函数f(x)=lnx,x∈(1,+∞)的图象在点(x0,lnx0)处的切线为l,若l与函数g(x)=$\frac{1}{2}$x2的图象相切,则x0必满足( )
(ln2≈0.6931,ln3≈1.0986)
(ln2≈0.6931,ln3≈1.0986)
| A. | 1<x0<$\sqrt{2}$ | B. | $\sqrt{2}$<x0<2 | C. | 2<x0<3 | D. | 3<x0<4 |
2.定义在R上的函数f(x)的图象关于直线x=2对称,且f(x)满足:对任意的x1,x2∈(-∞,2](x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$,且f(4)=0,则关于x不等式$\frac{f(x)}{x}<0$的解集是( )
| A. | (-∞,0)∪(4,+∞) | B. | (0,2)∪(4,+∞) | C. | (-∞,0)∪(0,4) | D. | (0,2)∪(2,4) |
3.设A(-5,0),B(5,0),M为平面上的动点,若当|MA|-|MB|=10时,M的轨迹为( )
| A. | 双曲线的一支 | B. | 一条线段 | C. | 一条射线 | D. | 两条射线 |
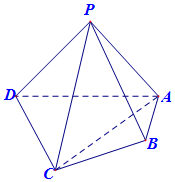 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.