题目内容
在双曲线(1)求y1+y2的值;
(2)证明线段AC的垂直平分线经过定点,并求出定点的坐标.
分析:对于(1),由于(x1,y1)、(x2,y2)均在![]() 上,因此可以先将x1和y1当作已知数,分别求出|BF|、|AF|和|CF|,然后运用等差中项知识求解;另外,AF、BF、CF是双曲线的焦半径,亦可用焦半径公式求解.对于(2)应先写出垂直平分线方程,由于A、C是动点,故垂直平分线方程中必含有字母系数,再讨论直线过哪一个与字母无关的定点.
上,因此可以先将x1和y1当作已知数,分别求出|BF|、|AF|和|CF|,然后运用等差中项知识求解;另外,AF、BF、CF是双曲线的焦半径,亦可用焦半径公式求解.对于(2)应先写出垂直平分线方程,由于A、C是动点,故垂直平分线方程中必含有字母系数,再讨论直线过哪一个与字母无关的定点.
解:(1)依题意可知,点A、B、C同在双曲线的上支,又上焦点对应的上准线方程为y=![]() ,离心率为e,根据双曲线第二定义,知
,离心率为e,根据双曲线第二定义,知
|AF|=e(y1-![]() ),|BF|=e(6-
),|BF|=e(6-![]() ),|CF|=e(y2-
),|CF|=e(y2-![]() ).
).
由于|AF|、|BF|、|CF|成等差数列,
故有|AF|+|CF|=2|BF|,
即e(y1-![]() )+e(y2-
)+e(y2-![]() )=2e(6-
)=2e(6-![]() ).
).
∴y1+y2=12.
(2)设AC的中点为M(x0,y0),AC的垂直平分线为l,斜率为k,则有y0=![]() 分 y1+y2[]2式=6,l的方程为y=k(x-x0)+6, ①
分 y1+y2[]2式=6,l的方程为y=k(x-x0)+6, ①

②-③,得13(y12-y22)-12(x12-x22)=0,
即13(y1-y2)(y1+y2)-12(x1-x2)(x1+x2)=0.
∴13×12(y1-y2)-12×2(x1-x2)x0=0.
∴![]()
∴![]()
∴AC的垂直平分线方程为![]()
若使上式对一切实数k恒成立,则x=0,y=![]() ,即直线l过定点(0,
,即直线l过定点(0,![]() ).
).
绿色通道:
遇到焦点的弦的问题或双曲线上的点到焦点的距离的问题,要注意焦半径公式的应用.
对于直线过定点问题,一般利用相交直线系方程y-y0=k(x-x0)的形式来求定点.

练习册系列答案
相关题目
 的一支上不同的三点A(x1,y1)、B(
的一支上不同的三点A(x1,y1)、B(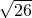 ,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.
,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列. 的一支上不同的三点A(x1,y1)、B(
的一支上不同的三点A(x1,y1)、B( ,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.
,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.