题目内容
在双曲线 的一支上不同的三点A(x1,y1)、B(
的一支上不同的三点A(x1,y1)、B( ,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.
,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.(1)求y1+y2;
(2)证明线段AC的垂直平分线经过某一定点,并求该定点的坐标.
【答案】分析:(1)由双曲线的焦半径公式可知|AF|= ,|BF|=
,|BF|= ,|CF|=
,|CF|= ,再由|AF|,|BF|,|CF|成等差数列,可求出y1+y2的值.
,再由|AF|,|BF|,|CF|成等差数列,可求出y1+y2的值.
(2)借助点差法求出AC的垂直平分线方程为 ,由此可以得到不论
,由此可以得到不论 为何值,直线恒过定点
为何值,直线恒过定点 .
.
解答:解:(1)由题设知,A、B、C在双曲线的同一支上,且y1,y2均大于0,
∴由双曲线的焦半径公式可知|AF|= ,|BF|=
,|BF|= ,|CF|=
,|CF|= ,
,
∵|AF|,|BF|,|CF|成等差数列,∴ ,
,
∴y1+y2=12.
(2)证明:∵A,C在双曲线上,∴ ,且
,且 .两式相减得
.两式相减得 ,
,
于是AC的垂直平分线方程为 ,即
,即 ,
,
∴y=- .
.
∴不论 为何值,直线恒过定点
为何值,直线恒过定点 .
.
点评:本题考查双曲线的性质及其运用,解题时要注意点差法的合理应用.
 ,|BF|=
,|BF|= ,|CF|=
,|CF|= ,再由|AF|,|BF|,|CF|成等差数列,可求出y1+y2的值.
,再由|AF|,|BF|,|CF|成等差数列,可求出y1+y2的值.(2)借助点差法求出AC的垂直平分线方程为
 ,由此可以得到不论
,由此可以得到不论 为何值,直线恒过定点
为何值,直线恒过定点 .
.解答:解:(1)由题设知,A、B、C在双曲线的同一支上,且y1,y2均大于0,
∴由双曲线的焦半径公式可知|AF|=
 ,|BF|=
,|BF|= ,|CF|=
,|CF|= ,
,∵|AF|,|BF|,|CF|成等差数列,∴
 ,
,∴y1+y2=12.
(2)证明:∵A,C在双曲线上,∴
 ,且
,且 .两式相减得
.两式相减得 ,
,于是AC的垂直平分线方程为
 ,即
,即 ,
,∴y=-
 .
.∴不论
 为何值,直线恒过定点
为何值,直线恒过定点 .
.点评:本题考查双曲线的性质及其运用,解题时要注意点差法的合理应用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 的一支上不同的三点A(x1,y1)、B(
的一支上不同的三点A(x1,y1)、B(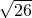 ,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.
,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.