题目内容
在双曲线(1)求y1+y3的值;
(2)求证:线段AC的垂直平分线经过某一定点,并求出定点坐标.
(1)解:∵ ,
,
∴|PF|=ey-a.又A、B、C到F的距离成等差数列,∴2(ey2-a)=(ey1-a)+(ey3-a).
∴y1+y3=2y2=12.
(2)证明:由题意,得
①-②,得![]() (y1-y3)(y1+y3)-
(y1-y3)(y1+y3)-![]() (x1-x3)·(x1+x3)=0.
(x1-x3)·(x1+x3)=0.
∴![]() =
=![]() =
=![]() .
.
若x1+x3=0.
则kAC=0,y1=y3=y2=6,A、B、C三点共线,这是不可能的.
∴x1+x3≠0.则AC的中垂线方程为y-6=![]() (x-
(x-![]() ),
),
即y=![]() .因此,AC的中垂线过定点(0,
.因此,AC的中垂线过定点(0,![]() ).
).

练习册系列答案
相关题目
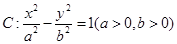 与椭圆
与椭圆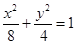 有公共焦点,且以抛物线
有公共焦点,且以抛物线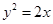 的准线为双曲线
的准线为双曲线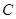 的一条准线.动直线
的一条准线.动直线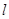 过双曲线
过双曲线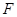 且与双曲线的右支交于
且与双曲线的右支交于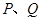 两点.
两点.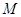 ,使
,使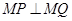 恒成立?若存在,求出点
恒成立?若存在,求出点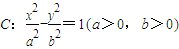 与椭圆
与椭圆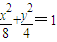 有公共焦点,且以抛物线y2=2x的准线为双曲线C的一条准线.动直线l过双曲线C的右焦点F且与双曲线的右支交于P、Q两点.
有公共焦点,且以抛物线y2=2x的准线为双曲线C的一条准线.动直线l过双曲线C的右焦点F且与双曲线的右支交于P、Q两点.