题目内容
已知函数 (
(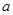 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数 是区间[-1,1]上的减函数
是区间[-1,1]上的减函数
(I)求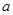 的值;
的值;
(II)求 的取值范围;
的取值范围;
(III)若 在
在 上恒成立,求
上恒成立,求 的取值范围。
的取值范围。
(1) 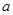 ="0." (2)
="0." (2)
解析试题分析:解:(Ⅰ) 函数
函数 是实数集R上的奇函数,
是实数集R上的奇函数,
 所以
所以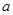 =0. 3分
=0. 3分
(Ⅱ) 是区间[-1,1]上的减函数
是区间[-1,1]上的减函数 在[-1,1]上恒成立
在[-1,1]上恒成立
 . 5分
. 5分
又
 ,
,
 .
.
 . 8分
. 8分
(Ⅲ)
 在区间[-1,1]上单调递减,
在区间[-1,1]上单调递减,
 .
.
只需 .
.
 恒成立. 10分
恒成立. 10分
令 ,
,
则 12分
12分

而 恒成立,
恒成立, 
 . 14分
. 14分
考点:本试题考查了导数的知识。
点评:对于导数在函数中的作用,主要是解决函数的单调性的运用,同时要结合不等式恒成立,分离参数发,构造新函数,通过函数的最值来分析得到参数的取值范围问题,这是高考的一个热点,要加以关注。而这类问题的处理方法既可以分离也可以不分离来做,因题而异。属于中档题。

练习册系列答案
相关题目
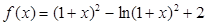 .
. 的单调增区间;
的单调增区间;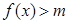 在
在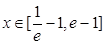 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.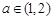 ,总存在
,总存在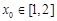 ,使不等式
,使不等式 成立,求实数m的取值范围.
成立,求实数m的取值范围. (
(
 R).
R). ,求函数
,求函数 的极值;
的极值; 上有两个零点,若存在,求出
上有两个零点,若存在,求出 。
。 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数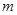 的取值范围。
的取值范围。

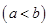 ,使得函数
,使得函数 的定义域、值域都是
的定义域、值域都是 ,若存在,则求出
,若存在,则求出 (
(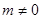 ),求
),求 的取值范围.
的取值范围. ,函数
,函数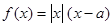 .
. 在
在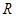 上的奇偶性;
上的奇偶性; 上的最大值。
上的最大值。 .
.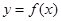 在
在 和
和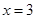 处的切线互相平行,求
处的切线互相平行,求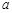 的值;
的值; 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 为奇函数,当
为奇函数,当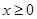 时,
时, (如图).
(如图).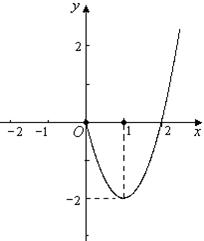
 在区间
在区间 上单调递增.
上单调递增. 的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为
的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为 ,容积为
,容积为 .
.