题目内容
(本小题满分12分)
已知函数
(1)是否存在实数
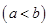 ,使得函数
,使得函数 的定义域、值域都是
的定义域、值域都是 ,若存在,则求出
,若存在,则求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(2)若存在实数
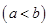 ,使得函数
,使得函数 的定义域为
的定义域为 时,值域为
时,值域为 (
(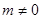 ),求
),求 的取值范围.
的取值范围.
(1) 不存在适合条件的实数 (2)
(2) 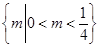
解析试题分析:解:(1)若存在满足条件的实数 ,使得函数
,使得函数 的定义域、值域都是
的定义域、值域都是 ,则
,则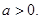 由题意知
由题意知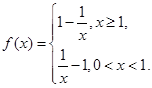

① 当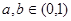 时,
时,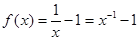 在
在 上为减函数.故
上为减函数.故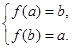 即
即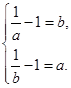 解得
解得 ,故此时不存在适合条件的实数
,故此时不存在适合条件的实数
②当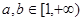 时,
时,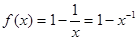 在
在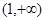 上是增函数. 故
上是增函数. 故 即
即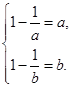 ,此时
,此时 是方程
是方程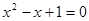 的根,此方程无实根.故此时不存在适合条件的实数
的根,此方程无实根.故此时不存在适合条件的实数
③当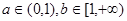 时, 由于
时, 由于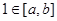 ,而
,而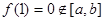 ,故此时不存在适合条件的实数
,故此时不存在适合条件的实数 ,综上可知,不存在适合条件的实数
,综上可知,不存在适合条件的实数 .
.
(2)若存在实数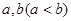 ,使得函数
,使得函数 的定义域为
的定义域为 时,值域为
时,值域为
则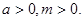
①当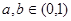 时,由于
时,由于 在
在 上是减函数,值域为
上是减函数,值域为 ,
,
即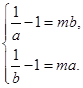 此时
此时 异号,不合题意.所以
异号,不合题意.所以 不存在.
不存在.
②当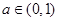 或
或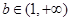 时,由(1)知0在值域内,值域不可能是
时,由(1)知0在值域内,值域不可能是 ,所以
,所以 不存在,故只有
不存在,故只有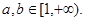
又因为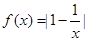 在
在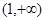 上是增函数,
上是增函数,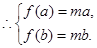 即
即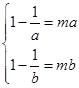
 是方程
是方程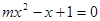 的两个根,即关于
的两个根,即关于 的方程
的方程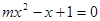 有两个大于
有两个大于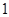 的实根.设这两个根为
的实根.设这两个根为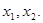 则
则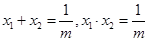
所以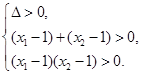 即
即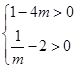 解得
解得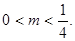
故 的取值范围是
的取值范围是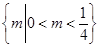
考点:本试题考查了函数的概念运用。
点评:解决函数的定义域和值域的问题,主要是分析函数的单调性,对于含有绝对值的 函数实际就是分段函数,要分别考虑求解其值域,同时要注意分段函数的值域等于各段函数值域的并集,定义域也是各段定义域的并集,属于难度试题。

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 .
.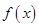 的图象,写出函数
的图象,写出函数 的不等式
的不等式
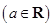 .
.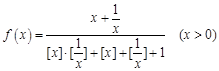 ,其中
,其中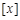 表示不超过
表示不超过 的最大整数,如
的最大整数,如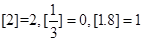 .
.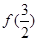 的值;
的值;  上存在x,使得
上存在x,使得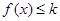 成立,求实数k的取值范围;
成立,求实数k的取值范围; 的值域.
的值域. 
 上是增函数还是减函数?并用定义证明.
上是增函数还是减函数?并用定义证明.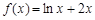 ,
,
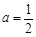 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: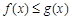 .
. (
(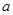 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数 是区间[-1,1]上的减函数
是区间[-1,1]上的减函数 的取值范围;
的取值范围; 在
在 上恒成立,求
上恒成立,求 的取值范围。
的取值范围。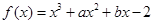 的图象过点
的图象过点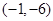 ,且函数
,且函数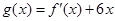 的图象关于
的图象关于 轴对称;
轴对称;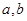 的值及函数
的值及函数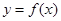 的单调区间;
的单调区间;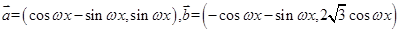 ,设函数
,设函数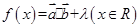 的图象关于直线
的图象关于直线 =π对称,其中
=π对称,其中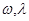 为常数,且
为常数,且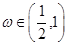 .
. 的最小正周期;
的最小正周期;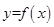 的图象经过点
的图象经过点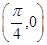 ,求函数
,求函数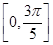 上的取值范围.
上的取值范围.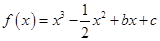 ,且
,且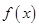 在
在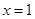 处取得极值.
处取得极值.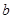 的值;
的值;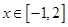 时,
时,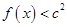 恒成立,求
恒成立,求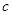 的取值范围;
的取值范围;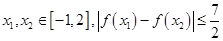 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.