题目内容
已知各项均为正实数的数列{an}的前n项和为Sn,4Sn=an2+2an-3对于一切n∈N*成立。
(1)求a1;
(2)求数列{an}的通项公式;
(3)设bn=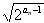 ,Tn为数列的
,Tn为数列的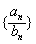 前n项和,求证:Tn<5。
前n项和,求证:Tn<5。
(1)求a1;
(2)求数列{an}的通项公式;
(3)设bn=
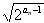 ,Tn为数列的
,Tn为数列的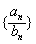 前n项和,求证:Tn<5。
前n项和,求证:Tn<5。解:(1)当n=1时,
得
解得 或
或
由条件知
所以 ;
;
(2)当 时,
时,
则
所以


由条件知
所以
故正实数的数列{an}是首项为3,公差为2的等差数列,
所以an=2n+1。
(3)由(2)知
∴ ①
①
将上式两边同乘以 得
得
 ②
②
①-②,得

即
∵
∴
∴ 。
。

得

解得
 或
或
由条件知

所以
 ;
;(2)当
 时,
时,
则

所以



由条件知

所以

故正实数的数列{an}是首项为3,公差为2的等差数列,
所以an=2n+1。
(3)由(2)知

∴
 ①
①将上式两边同乘以
 得
得  ②
②①-②,得

即

∵

∴

∴
 。
。
练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 为数列
为数列 的前n项和,求证Tn<5.
的前n项和,求证Tn<5.