题目内容
已知函数
，则f（x）在区间
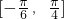上的最大值M和最小值m分别为
- A.
- B.
- C.
- D.
A
分析：将f（x）=2cosxsin（x+
）-
化简为f（x）=sin（2x+），根据已知条件利用正弦函数的单调性即可求得最大值M和最小值m．
解答：∵f（x）=2cosxsin（x+）-
=2cosx[
sinx+cosx]-
=sin2x+
-
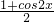=sin（2x+），
∵-≤x≤
，
∴-≤2x+≤
，
∴-≤sin（2x+）≤1．
∴M=1，m=-．
故选A．
点评：本题考查三角函数中的恒等变换应用，考查正弦函数的单调性与最值，属于中档题．
分析：将f（x）=2cosxsin（x+
）-化简为f（x）=sin（2x+），根据已知条件利用正弦函数的单调性即可求得最大值M和最小值m．解答：∵f（x）=2cosxsin（x+
）-=2cosx[
sinx+cosx]-=
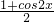sin2x+-=sin（2x+
），∵-
≤x≤，∴-
≤2x+≤，∴-
≤sin（2x+）≤1．∴M=1，m=-
．故选A．
点评：本题考查三角函数中的恒等变换应用，考查正弦函数的单调性与最值，属于中档题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
，则f（x）的定义域为 ．
，则f（x）（ ）
，则f（x）的值域为 ．
，则f（x）的图象关于（ ）对称．
，则f（x）的单调增区间为 ．