题目内容
若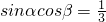 ,则sinβcosα的取值范围是________.
,则sinβcosα的取值范围是________.
[-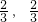 ]
]
分析:由sin(α+β)=sinαcosβ+cosαsinβ= +sinβcosα,sin(α-β)=sinαcosβ-cosαsinβ=
+sinβcosα,sin(α-β)=sinαcosβ-cosαsinβ= -sinβcosα,sin(α+β) sin(α-β)∈[-1,1],知-1
-sinβcosα,sin(α+β) sin(α-β)∈[-1,1],知-1 +sinβcosα≤1,由此能导出
+sinβcosα≤1,由此能导出 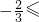 sinβcosα
sinβcosα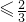 .
.
解答:sin(α+β)=sinαcosβ+cosαsinβ= +sinβcosα
+sinβcosα
sin(α-β)=sinαcosβ-cosαsinβ= -sinβcosα
-sinβcosα
sin(α+β) sin(α-β)∈[-1,1]
-1 +sinβcosα≤1
+sinβcosα≤1
- ≤sinβcosα
≤sinβcosα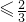 ,
,
-1 -sinβcosα≤1
-sinβcosα≤1
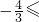 -sinβcosα
-sinβcosα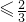 ,
,
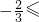 sinβcosα
sinβcosα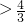 ,
,
所以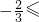 sinβcosα
sinβcosα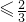 .
.
故答案为:[-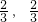 ].
].
点评:本题考查两角和与差的正弦函数,解题时要认真审题,仔细解答,注意三角函数的恒等变换.
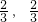 ]
]分析:由sin(α+β)=sinαcosβ+cosαsinβ=
 +sinβcosα,sin(α-β)=sinαcosβ-cosαsinβ=
+sinβcosα,sin(α-β)=sinαcosβ-cosαsinβ= -sinβcosα,sin(α+β) sin(α-β)∈[-1,1],知-1
-sinβcosα,sin(α+β) sin(α-β)∈[-1,1],知-1 +sinβcosα≤1,由此能导出
+sinβcosα≤1,由此能导出 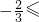 sinβcosα
sinβcosα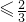 .
.解答:sin(α+β)=sinαcosβ+cosαsinβ=
 +sinβcosα
+sinβcosα sin(α-β)=sinαcosβ-cosαsinβ=
 -sinβcosα
-sinβcosαsin(α+β) sin(α-β)∈[-1,1]
-1
 +sinβcosα≤1
+sinβcosα≤1-
 ≤sinβcosα
≤sinβcosα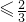 ,
,-1
 -sinβcosα≤1
-sinβcosα≤1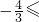 -sinβcosα
-sinβcosα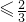 ,
,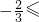 sinβcosα
sinβcosα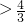 ,
,所以
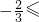 sinβcosα
sinβcosα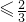 .
.故答案为:[-
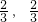 ].
].点评:本题考查两角和与差的正弦函数,解题时要认真审题,仔细解答,注意三角函数的恒等变换.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,则sinθ+cosθ= .
,则sinθ+cosθ= . ,则sinα+cosα的值为( )
,则sinα+cosα的值为( )


