题目内容
设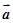 是已知的平面向量,向量
是已知的平面向量,向量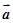 ,
, ,
, 在同一平面内且两两不共线,有如下四个命题:
在同一平面内且两两不共线,有如下四个命题:
①给定向量 ,总存在向量
,总存在向量 ,使
,使 ;
;
②给定向量 和
和 ,总存在实数
,总存在实数 和
和 ,使
,使 ;
;
③给定单位向量 和正数
和正数 ,总存在单位向量
,总存在单位向量 和实数
和实数 ,使
,使 ;
;
④若 =2,存在单位向量
=2,存在单位向量 、
、 和正实数
和正实数 ,
, ,使
,使 ,则
,则
其中真命题是____________.
①②④
解析试题分析:给定向量 ,总存在向量
,总存在向量 ,使
,使 ,即
,即 .显然存在
.显然存在 .所以①正确.由平面向量的基本定理可得②正确.给定单位向量
.所以①正确.由平面向量的基本定理可得②正确.给定单位向量 和正数
和正数 ,总存在单位向量
,总存在单位向量 和实数
和实数 ,使
,使 ,当
,当 分解到
分解到 方向的向量长度大于
方向的向量长度大于 时,向量
时,向量 没办法按
没办法按 分解,所以③不正确.存在单位向量
分解,所以③不正确.存在单位向量 、
、 和正实数
和正实数 ,
, ,由于
,由于 ,向量
,向量 、
、 的模为1,由三角形的三边关系可得
的模为1,由三角形的三边关系可得 ..由
..由 .所以④成立.综上①②④.
.所以④成立.综上①②④.
考点:1.向量的运算.2平面向量的基本定理.3.基本不等式.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
设向量 ,
, ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. | C. ∥ ∥ | D. 与 与 垂直 垂直 |
已知 =(x,2),
=(x,2), =(1,x),若
=(1,x),若 //
// ,则x的值为( )
,则x的值为( )
A.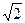 | B. | C.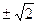 | D.2 |
已知 ="(2,3)," b=(-4,7),则
="(2,3)," b=(-4,7),则 在b上的投影为( )
在b上的投影为( )
A. | B. | C. | D. |
如图1,D,E,F分别是 ABC的边AB,BC,CA的中点,则
ABC的边AB,BC,CA的中点,则
A. |
B. |
C. |
D. |
 经过点
经过点 ,方向向量为
,方向向量为 ,则直线
,则直线 ,若
,若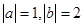 ,当且仅当
,当且仅当 时,
时, 取得最小值,则向量a、b的夹角为___________.
取得最小值,则向量a、b的夹角为___________. ,设
,设 ∥
∥ ,若
,若
 ,则
,则 的值为 .
的值为 .
 的最小值是 .
的最小值是 .