题目内容
12.已知在△ABC中,角A,B,C的对边分别是a,b,c,且cos(2B+2C)-3cos(B+C)=1.(1)求角A的大小;
(2)若a=2,△ABC的面积S=$\frac{\sqrt{3}}{2}$,求b+c的值.
分析 (1)cos(2B+2C)-3cos(B+C)=1,利用倍角公式与诱导公式即可得出.
(2)由于△ABC的面积S=$\frac{\sqrt{3}}{2}$=$\frac{1}{2}bcsinA$,化为bc=2.再利用余弦定理可得:a2=b2+c2-2bccosA=(b+c)2-2bc-2bccosA,即可得出.
解答 解:(1)cos(2B+2C)-3cos(B+C)=1,化为2cos2(B+C)-1-3cos(B+C)=1,
∴2cos2A+3cosA-2=0,cosA∈(0,-1),解得cosA=$\frac{1}{2}$,A∈(0,π),
∴$A=\frac{π}{3}$.
(2)∵△ABC的面积S=$\frac{\sqrt{3}}{2}$=$\frac{1}{2}bcsinA$=$\frac{1}{2}bcsin\frac{π}{3}$,化为bc=2.
利用余弦定理可得:a2=b2+c2-2bccosA=(b+c)2-2bc-2bccosA,
∴22=(b+c)2-2×2cos$\frac{π}{3}$,可得:b+c=$\sqrt{6}$.
点评 本题考查了倍角公式与诱导公式、余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.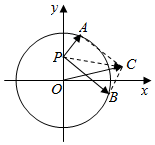 如图,已知点P(0,$\frac{\sqrt{2}}{3}$),点A,B是单位圆O上的两个动点,若$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,动点C满足$\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB}$,则关于|$\overrightarrow{OC}$|的说法正确的是( )
如图,已知点P(0,$\frac{\sqrt{2}}{3}$),点A,B是单位圆O上的两个动点,若$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,动点C满足$\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB}$,则关于|$\overrightarrow{OC}$|的说法正确的是( )
 如图,已知点P(0,$\frac{\sqrt{2}}{3}$),点A,B是单位圆O上的两个动点,若$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,动点C满足$\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB}$,则关于|$\overrightarrow{OC}$|的说法正确的是( )
如图,已知点P(0,$\frac{\sqrt{2}}{3}$),点A,B是单位圆O上的两个动点,若$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,动点C满足$\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB}$,则关于|$\overrightarrow{OC}$|的说法正确的是( )| A. | |$\overrightarrow{OC}$|随点A,B位置的改变而变化,且最大值为$\frac{4}{3}$ | |
| B. | |$\overrightarrow{OC}$|随点A,B位置的改变而变化,且最小值为$\frac{4}{3}$ | |
| C. | |$\overrightarrow{OC}$|是一个常数,且值为$\frac{4}{3}$ | |
| D. | 以上说法都不对 |
4.已知定义在[3m-1,m]的函数f(x)=-mx2+(n+1)x,且f(x-2)是偶函数,则(n-m)2=( )
| A. | 0 | B. | $\frac{25}{16}$ | C. | $\frac{121}{16}$ | D. | 16 |