题目内容
△ABC中,己知∠A>∠B>∠C,且∠A=2∠C,b=4,a+c=8,求a,c的长.
分析:根据正弦定理得
=
,结合已经条件算出sin2C+sinC=2sin3C,利用两角和的正弦公式和二倍角公式化简整理,得8cos2C-2cosC-3=0,解出锐角C的余弦值为
.最后利用余弦定理建立关系式,结合a+c=8即可解出边a、c的长.
| b |
| sinB |
| a+c |
| sinA+sinC |
| 3 |
| 4 |
解答:解:根据正弦定理
=
=
,得
=
∵b=4,a+c=8,∠A=2∠C,
∴
=
,可得sin2C+sinC=2sin(π-3C)=2sin3C
∵sin2C=2sinCcosC,sin3C=sin(2C+C)=sin2CcosC+cos2CsinC=2sinCcos2C+sinC(2cos2C-1)
∴2sinCcosC+sinC=2[2sinCcos2C+sinC(2cos2C-1)]
结合sinC>0,化简整理得:8cos2C-2cosC-3=0,
解之得cosC=
或cosC=-
∵∠A>∠B>∠C,得C为锐角,
∴cosC=-
不符合题意,舍去
根据余弦定理,得cosC=
=
,
∴
=
,解之得a=
,c=8-a=
综上,a、c的长分别为
、
.
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| b |
| sinB |
| a+c |
| sinA+sinC |
∵b=4,a+c=8,∠A=2∠C,
∴
| 4 |
| sin(π-3C) |
| 8 |
| sin2C+sinC |
∵sin2C=2sinCcosC,sin3C=sin(2C+C)=sin2CcosC+cos2CsinC=2sinCcos2C+sinC(2cos2C-1)
∴2sinCcosC+sinC=2[2sinCcos2C+sinC(2cos2C-1)]
结合sinC>0,化简整理得:8cos2C-2cosC-3=0,
解之得cosC=
| 3 |
| 4 |
| 1 |
| 2 |
∵∠A>∠B>∠C,得C为锐角,
∴cosC=-
| 1 |
| 2 |
根据余弦定理,得cosC=
| a2+b2-c2 |
| 2ab |
| 3 |
| 4 |
∴
| a2+42-(8-a)2 |
| 2×a×4 |
| 3 |
| 4 |
| 24 |
| 5 |
| 16 |
| 5 |
综上,a、c的长分别为
| 24 |
| 5 |
| 16 |
| 5 |
点评:本题给出△ABC的最大角等于最小角的2倍,最大边与最小边之和等于第三边的2倍,求边a、c的长.着重考查了三角恒等变换和利用正余弦定理解三角形的知识,属于中档题.

练习册系列答案
相关题目
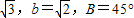 ,则角A的值为( )
,则角A的值为( )