题目内容
3.已知A={(x,y)|x-2y=0},B={(x,y)|$\frac{y-1}{x-2}$=0},则A∪B等于( )| A. | {(x,y)|(x-2y)(y-1)=0} | B. | {(x,y)|(x-2y)(y-1)=0,x≠2} | ||
| C. | {(2,1)} | D. | ∅ |
分析 先化简集合B,易知点(2,1)的坐标适合方程x-2y=0,所以点(2,1)在集合A内,两个集合再取并集
解答 解:∵B={(x,y)|$\frac{y-1}{x-2}$=0}={(x,y)|y=1,x≠2},(2,1)∈A.
∴A∪B={(x,y)|(x-2y)(y-1)=0},
故选:A
点评 本题主要考查集合的并集运算.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
18.${sin^2}\frac{π}{12}-{cos^2}\frac{π}{12}$的结果是( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
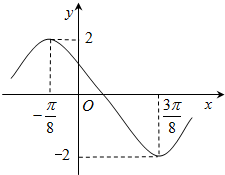 已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.