题目内容
曲线y=x2+4x+2在点x=-1处的切线方程为（ ）A．y=2x+1
B．y=2x-1
C．y=-2x-3
D．y=-2x-2
【答案】分析：首先可求出切点为（-1-1）然后再利用导数的几何意义求出曲线y=x2+4x+2在点x=-1处的切线的斜率为f′（-1）最后再根据点斜式写出切线方程即可．
解答：解：当x=-1时y=1-4+2=-1故切点为（-1，-1）
令y=f（x）=x2+4x+2
∴f′（x）=2x+4
∴根据导数的几何意义可得曲线y=x2+4x+2在点x=-1处的切线的斜率为f′（-1）=2
∴曲线y=x2+4x+2在点x=-1处的切线方程为y-（-1）=2（x+1）即y=2x+1
故选A
点评：本题主要考察了利用导数的几何意义求切线方程，属常考题，较易．解题的关键是利用导数的几何意义求出曲线y=x2+4x+2在点x=-1处的切线的斜率为f′（-1）！
解答：解：当x=-1时y=1-4+2=-1故切点为（-1，-1）
令y=f（x）=x2+4x+2
∴f′（x）=2x+4
∴根据导数的几何意义可得曲线y=x2+4x+2在点x=-1处的切线的斜率为f′（-1）=2
∴曲线y=x2+4x+2在点x=-1处的切线方程为y-（-1）=2（x+1）即y=2x+1
故选A
点评：本题主要考察了利用导数的几何意义求切线方程，属常考题，较易．解题的关键是利用导数的几何意义求出曲线y=x2+4x+2在点x=-1处的切线的斜率为f′（-1）！
练习册系列答案
相关题目
已知a，b，c，d成等比数列，且曲线y=x2-4x的顶点是（b，c），则ad等于（ ）
| A、8 | B、6 | C、-8 | D、4 |
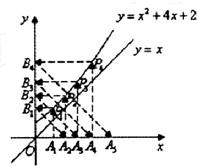如图，过点A1作垂直于x轴的垂线交曲线y=x2+4x+2于点P1，又过点P1作x轴的平行线交y轴于点B1，记点B1关于直线y=x的对称点为A2；…；依此类推．若数列{an}的各项分别为点列An（n=1，2，3…）的横坐标，且a1=1，则an=