题目内容
已知圆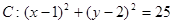 ,直线
,直线
(1)求证:直线恒过定点
(2)判断直线被圆 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时 的值及最短长度。
的值及最短长度。
(1)见解析(2)当直线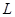 垂直于
垂直于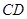 时被截得弦长最短,此时
时被截得弦长最短,此时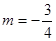 ,最短弦长为
,最短弦长为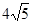
解析试题分析:(1)证明:直线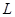 的方程
的方程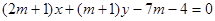 ,
,
经整理得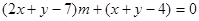 , ……1分
, ……1分
由 的任意性
的任意性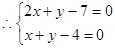 , ……3分
, ……3分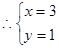
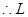 恒过定点
恒过定点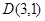 . ……5分
. ……5分
(2)解:因为直线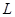 恒经过圆
恒经过圆 内一点
内一点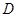 ,当直线
,当直线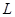 垂直于
垂直于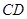 时被截得弦长最短. ……7分
时被截得弦长最短. ……7分
由 、
、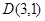 ,直线
,直线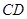 斜率
斜率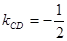 ,
,
又直线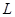 与直线
与直线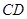 垂直,
垂直,  直线
直线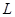 的斜率为2,
的斜率为2,
于是 ,
,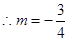 , ……9分
, ……9分
最短弦长为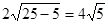 , ……11分
, ……11分
综上所述,当直线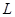 垂直于
垂直于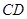 时被截得弦长最短,
时被截得弦长最短,
此时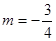 ,最短弦长为
,最短弦长为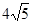 . ……12分
. ……12分
考点:本小题主要考查直线过定点、直线与圆的位置关系、弦长等问题,考查学生分析问题、解决问题的能力和运算求解能力.
点评:当直线与圆相交时,圆心到直线的距离、半弦长和半径组成一个直角三角形,这个直角三角形在解题时经常用到.

练习册系列答案
相关题目
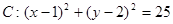 ,直线
,直线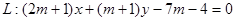
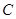 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时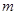 的值及最短长度。
的值及最短长度。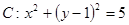 ,直线
,直线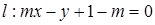
 恒过定点;
恒过定点;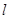 与圆交于
与圆交于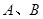 两点,若
两点,若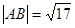 ,求直线
,求直线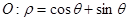 和直线
和直线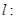
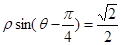 .
. 和直线
和直线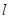 的直角坐标方程;
的直角坐标方程;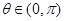 时,求直线
时,求直线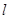 与圆
与圆