题目内容
a,b,c分别为角A,B,C的对边,S为△ABC的面积,且S=c2-(a-b)2,则tanC=______.
由余弦定理得S=c2-(a2+b2)+2ab=-2abcosC+2ab=2ab(1-cosC)=
absinC,
∴
=
,∴
=
,∴tan
=
,
∴tanC=
=
=
.
故答案
.
| 1 |
| 2 |
∴
| 1-cosC |
| sinC |
| 1 |
| 4 |
2sin2
| ||||
2sin
|
| 1 |
| 4 |
| C |
| 2 |
| 1 |
| 4 |
∴tanC=
2tan
| ||
1-tan2
|
2×
| ||
1-(
|
| 8 |
| 15 |
故答案
| 8 |
| 15 |

练习册系列答案
相关题目
 ,
, ,且
,且
 ,求实数b的值.
,求实数b的值.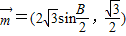 ,
,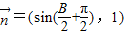 ,且
,且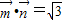
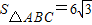 ,求实数b的值.
,求实数b的值.