题目内容

17．设3x-1，x，4x是等差数列{an}的前三项，则a4=$\frac{7}{5}$．

分析 由等差数列的性质列式求得x，进一步求出a3和d，则a4可求．

解答 解：∵3x-1，x，4x是等差数列{an}的前三项，
∴3x-1+4x=2x，解得：x=$\frac{1}{5}$，
∴${a}_{3}=\frac{4}{5}$，d=3x=$\frac{3}{5}$，
∴${a}_{4}={a}_{3}+d=\frac{7}{5}$．
故答案为：$\frac{7}{5}$．

点评 本题考查等差数列的性质，考查了等差数列的通项公式，是基础的计算题．

练习册系列答案
相关题目
7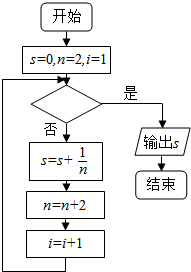．如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个流程图，其中判断框内应填入的条件是（　　）
A．i≤21B．i≤11C．i≥21D．i≥11
8．运行如图所示的程序框图，则输出的结果是（　　）
A．-2B．2C．5D．7
5．已知集合$A=\{x\left|{\frac{x-2}{x-7}＜0\}}\right.$，B={x|x2-12x+20＜0}，C={x|5-a＜x＜a}
（1）求集合A，B；   
（2）求A∪B，（∁RA）∩B；   
（3）若C⊆B，求实数a的取值范围．
12．设集合A={x|x2-5x-14＜0}，B={x|x＞1，x∈N}，则A∩B的元素的个数为（　　）
A．3B．4C．5D．6
2．已知函数$f（x）=\left\{\begin{array}{l}x-3，x＞0\\{3^x}，x≤0\end{array}\right.$，则f（f（2））的值是（　　）
A．$\frac{1}{3}$B．3C．$-\frac{1}{3}$D．-3
9．设函数f（x）=4sin（ωx+$\frac{π}{4}$）（ω＞0）的最小正周期为π，设向量$\overrightarrow{a}$=（-1，f（x）），$\overrightarrow{b}$=（f（-x），1），g（x）=$\overrightarrow{a}$•$\overrightarrow{b}$．
（1）求函数f（x）的递增区间；
（2）求函数g（x）在区间[$\frac{π}{8}$，$\frac{π}{3}$]上的最大值和最小值．
6．cos350°cos40°-sin190°cos50°=（　　）
A．$-\frac{1}{2}$B．$-\frac{{\sqrt{3}}}{2}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{1}{2}$
7．下列说法正确的是（　　）
A．若直线l平行于平面α内的无数条直线，则l∥α
B．若直线a在平面α外，则a∥α
C．若直线a∥b，b?α，则a∥α
D．若直线a∥b，b?α，则直线a平行于平面α内的无数条直线

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网