题目内容
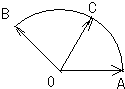（2011•重庆模拟）给定两个长度均为2的平面向量| OA |
| OB |
 |
| AB |
| OC |
| ||
| 3 |
| OA |
| OB |
分析：根据题意，建立坐标系，设出A，B点的坐标，并设∠AOC=α，则向量
=(2cosα，2sinα)，且
=
x
+y
，由向量相等，得x，y的值，从而求得x+y的最值．
| OC |
| OC |
| ||
| 3 |
| OA |
| OB |
解答：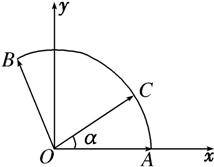
解：建立如图所示的坐标系，
则A（2，0），B（2cos150°，2sin150°），
即B（-
，1）．
设∠AOC=α，则
=（2cosα，2sinα）．
∵
=
x
+y
∴（
x，0）+（-
y，
y）=（cosα，sinα）．
∴
∴
∴x+y=5sinα+
cosα=2
sin（α+θ），（此时有tanθ=
，θ是个锐角）．
∵0°≤α≤150°．∴α+θ可取到90°．
∴x+y有最大值2
，
故选A
解：建立如图所示的坐标系，则A（2，0），B（2cos150°，2sin150°），
即B（-
| 3 |
设∠AOC=α，则
| OC |
∵
| OC |
| ||
| 3 |
| OA |
| OB |
∴（
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴
|
∴
|
∴x+y=5sinα+
| 3 |
| 7 |
| ||
| 5 |
∵0°≤α≤150°．∴α+θ可取到90°．
∴x+y有最大值2
| 7 |
故选A
点评：本题是向量的坐标表示的应用，结合图形，利用三角函数的性质，容易求出结果，本题解题的关键是建立坐标系，利用向量的坐标表示进行计算，本题综合性较经强．
练习册系列答案
相关题目
（2011•重庆模拟）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜π）的部分图象如图所示，则函数f（x）的解析式为（ ）