题目内容
已知函数![]() ,且
,且![]() 在(一∞,一1),(2,+∞)上单调递增,在(一1,2)上单调递减,又函数
在(一∞,一1),(2,+∞)上单调递增,在(一1,2)上单调递减,又函数![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求证当![]() 时,
时,![]() ;
;
(Ⅲ)若函数![]() ,求
,求![]() 的单调区间.
的单调区间.
解:(I)∵![]()
∴![]()
又函数![]() (―∞.―1).(2,+∞)上单调增。在(一1.2)上单调减
(―∞.―1).(2,+∞)上单调增。在(一1.2)上单调减
∴-1,2是方程![]() 的两个根
的两个根
从而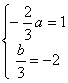
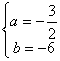
∴![]()
(Ⅱ)令![]() =
=![]()
∴ ![]()
∵![]() ∴
∴![]()
从而函效![]() 在(4,+∞)上单调增
在(4,+∞)上单调增
又H(4)=0
∴当![]() 时
时![]()
(Ⅲ)∵![]()
∴![]()
∴![]()
①当![]() ≤一2时,
≤一2时,![]() ≥2,定义域:(
≥2,定义域:( ![]() ,+∞)
,+∞)
![]() (
(![]() )
)![]() O恒成立,h(
O恒成立,h(![]() )在(
)在(![]() .+∞)上单增;
.+∞)上单增;
②当一2<![]() ≤一1时,2
≤一1时,2![]()
![]() ≥l,定义域:(
≥l,定义域:( ![]() ,2)U(2,+∞)
,2)U(2,+∞)
![]() (
(![]() )
)![]() O恒成立.h(
O恒成立.h(![]() )在(
)在(![]() ,2),(2,+∞)上单增;
,2),(2,+∞)上单增;
③当![]() >一l时,
>一l时, ![]()
![]() 1,定义域:(
1,定义域:( ![]() ,2)U(2,+∞)
,2)U(2,+∞)
由![]() (
(![]() )
)![]() 0得
0得![]()
![]() 1。由
1。由![]() (
(![]() )
)![]() O得
O得![]()
![]() 1.
1.
故在(1,2),(2.+∞)上单增;在(![]() ,1)上单减.
,1)上单减.
所以当![]() ≤--2时,h(
≤--2时,h(![]() )在(
)在(![]() ,+∞)上单增;
,+∞)上单增;
当--2<![]() ≤一1时,h(
≤一1时,h(![]() )在(
)在(![]() ,2),(2.+∞)上单增;
,2),(2.+∞)上单增;
当![]()
![]() 一l时,在(1,2),(2,+∞)上单增;在(
一l时,在(1,2),(2,+∞)上单增;在(![]() ,1)上单减
,1)上单减

练习册系列答案
相关题目
 ,且函数y=f(x)的图象相邻两条对称轴之间的距离为
,且函数y=f(x)的图象相邻两条对称轴之间的距离为 .
. 的值;
的值; 在区间
在区间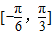 上单调递增,求实数k的取值范围;
上单调递增,求实数k的取值范围; 内仅有一解,若存在,求出实数m的取值范围,若不存在,说明理由.
内仅有一解,若存在,求出实数m的取值范围,若不存在,说明理由.