题目内容
5.设二次函数f(x)满足:f(0)=-1,f(x)-2=0的两根分别为-3和1.(1)求f(x)的解析式.
(2)在区间[0,2]上,y=f(x)的图象恒在直线y=kx-3的上方,求k的范围.
分析 (1)根据f(x)-2=0的两根分别为-3和1,可设f(x)-2=a(x+3)(x-1),将(0,-1)代入整理可得f(x)的解析式.
(2)在区间[0,2]上,y=f(x)的图象恒在直线y=kx-3的上方,即k<x+$\frac{2}{x}$+2恒成立,结合对勾函数的图象和性质,可得k的范围.
解答 解:(1)∵f(x)-2=0的两根分别为-3和1,
∴f(x)-2=a(x+3)(x-1),
又由f(0)=-1,
∴a=1,
∴f(x)-2=(x+3)(x-1),
即f(x)=x2+2x-1,
(2)若在区间[0,2]上,y=f(x)的图象恒在直线y=kx-3的上方,
则在区间[0,2]上,x2+2x-1>kx-3恒成立,
当x=0时,不等式显然成立,
当x∈(0,2]时,k<x+$\frac{2}{x}$+2恒成立,
令g(x)=x+$\frac{2}{x}$+2,由对勾函数图象和性质,可得当x=$\sqrt{2}$时,函数g(x)取最小值2+2$\sqrt{2}$,
故k<2+2$\sqrt{2}$.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
15.已知抛物线y=$\frac{{x}^{2}}{4}$与直线y=$\frac{3}{4}$x+1交于点P,Q,则如图所示阴影部分的面积为( )
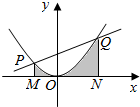

| A. | $\frac{65}{12}$ | B. | $\frac{85}{16}$ | C. | $\frac{143}{24}$ | D. | $\frac{95}{6}$ |
13. 学校组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了8次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
学校组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了8次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
(1)用茎叶图表示这两组数据;
(2)从统计学的角度考虑,你认为选派那位学生参加比赛合适,请说明理由?
(3)若将频率视为概率,对甲同学在今后的三次比赛成绩进行预测,记这三次成绩高于79个/分钟的次数为ξ,求ξ的分布列及数学期望Eξ.
(参考数据:22+12+112+102+62+72+12+22=316,02+112+122+22+52+52+42+32)
 学校组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了8次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
学校组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了8次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)| 甲 | 80 | 81 | 93 | 72 | 88 | 75 | 83 | 84 |
| 乙 | 82 | 93 | 70 | 84 | 77 | 87 | 78 | 85 |
(2)从统计学的角度考虑,你认为选派那位学生参加比赛合适,请说明理由?
(3)若将频率视为概率,对甲同学在今后的三次比赛成绩进行预测,记这三次成绩高于79个/分钟的次数为ξ,求ξ的分布列及数学期望Eξ.
(参考数据:22+12+112+102+62+72+12+22=316,02+112+122+22+52+52+42+32)
17.某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.
(1)求这些数据的线性回归方程;
(2)预测当广告费支出为9百万元时的销售额.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)求这些数据的线性回归方程;
(2)预测当广告费支出为9百万元时的销售额.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
14.已知函数f(x)=ex-1,g(x)=-x2+4x-3,若f(a)=g(b),则b的取值范围是( )
| A. | $[2-\sqrt{2},2+\sqrt{2}]$ | B. | $(2-\sqrt{2},2+\sqrt{2})$ | C. | [1,3] | D. | (1,3) |
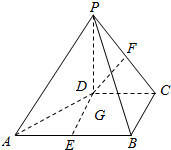 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.