题目内容

若方程
x2
k-2
+
y2
5-k
=1表示双曲线，则实数k的取值范围是
 
．
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：依题意，（k-5）（k-2）＜0，从而可得答案．
解答： 解：∵方程
x2
k-2
+
y2
5-k
=1表示双曲线，
∴（5-k）（k-2）＜0，
∴（k-5）（k-2）＞0，
∴k＞5或k＜2．
即k的取值范围为（-∞，2）∪（5，+∞）．
故答案为：（-∞，2）∪（5，+∞）．
点评：本题考查双曲线的简单性质，得到（5-k）（k-2）＜0是关键，属于基础题．
练习册系列答案
相关题目
已知函数，f（x）=x2+lnx-ax．
（Ⅰ）当a=3时，求f（x）的单调区间；
（Ⅱ）若f（x）在（0，1）上有极值，求a的取值范围；
（Ⅲ）在（Ⅱ）的结论下，设g（x）=1+x|x-a|（1≤x≤3），求函数g（x）的最大值．
已知函数f（x）=log
1
2
（x2-ax+2）
（1）a=3，求函数的定义域和值域．
（2）求实数a的取值范围，使得f（x）在（3，+∞）上是单调减函数．
解不等式：x（x-1）＜x（2x-3）+2．
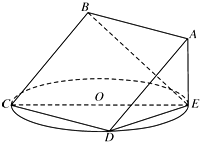如图，正方形ABCD所在平面与圆O所在平面相交于CD，线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C、D的点．
（Ⅰ）求证：CD⊥面ADE；
（Ⅱ）求证：平面ABCD⊥平面ADE．
数列{an}中，若a1=1，an+1=2an-3（n≥1），则该数列的通项an=
 
．
重庆一中高三有理科生高中生1200人，文科生400人，现用分层抽样的方法从所有师生中抽取一个容量为N的样本；已知从文科生中抽取人数为50人，那么N=
 
．
某程序框图如图所示，若输入一个小于10的正整数n，则该程序运行后输出n的值是
 
．
棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网