题目内容
f(x)=|x-2|-
在定义域内的零点个数为( )
| log | x2 |
| A.0 | B.2 | C.1 | D.3 |
∵f(x)=|x-2|-
,求其零点,
∴f(x)=0,
可得|x-2|=
,令g(x)=|x-2|,h(x)=
,g(x)与h(x)图象有交点,如下图
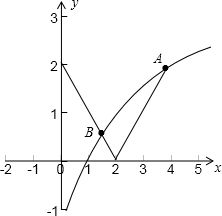
可知g(x)与h(x)交与两点A,B,
说明f(x)=|x-2|-
在定义域内的零点个数为2,
故选B.
| log | x2 |
∴f(x)=0,
可得|x-2|=
| log | x2 |
| log | x2 |

可知g(x)与h(x)交与两点A,B,
说明f(x)=|x-2|-
| log | x2 |
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
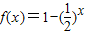 是[-1,0]上的一阶回归函数
是[-1,0]上的一阶回归函数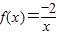 是(0,+∞)上的二阶回归函数;
是(0,+∞)上的二阶回归函数;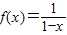 是(2,+∞)上的三阶回归函数.
是(2,+∞)上的三阶回归函数. 是[-1,0]上的一阶回归函数
是[-1,0]上的一阶回归函数 是(0,+∞)上的二阶回归函数;
是(0,+∞)上的二阶回归函数; 是(2,+∞)上的三阶回归函数.
是(2,+∞)上的三阶回归函数.