题目内容
定义:若{y|y=f(x),x∈A}=A,则f(x)称为A上的一阶回归函数;若{y|y=f(f(x)),x∈A}=A,则f(x)称为A上的二阶回归函数;
若{y|y=f(f(f(x))),x∈A}=A,则f(x)称为A上的三阶回归函数.
下列判断正确的个数是( )
①f(x)=3-x是[1,2]上的一阶回归函数;
②
 是[-1,0]上的一阶回归函数
是[-1,0]上的一阶回归函数③
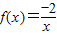 是(0,+∞)上的二阶回归函数;
是(0,+∞)上的二阶回归函数;④
 是(2,+∞)上的三阶回归函数.
是(2,+∞)上的三阶回归函数.A.1个
B.2个
C.3个
D.4个
【答案】分析:根据一阶回归函数的概念,分别判断f(x)=3-x在[1,2]上和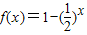 在[-1,0]上,是否满足定义可判断①②的真假;根据二阶回归函数的概念,判断
在[-1,0]上,是否满足定义可判断①②的真假;根据二阶回归函数的概念,判断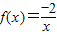 在(0,+∞)上是否满足定义可判断③的真假;根据三阶回归函数的概念,判断
在(0,+∞)上是否满足定义可判断③的真假;根据三阶回归函数的概念,判断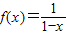 在(2,+∞)上是否满足定义可判断④的真假;
在(2,+∞)上是否满足定义可判断④的真假;
解答:解:∵f(x)=3-x在[1,2]上单调递减,∴当x=1时,f(x)取最大值2,当x=2时,f(x)取最小值1,
即{y|y=f(x)=3-x,x∈[1,2]}=[1,2],故①中函数是一阶回归函数,故①正确;
∵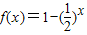 在[-1,0]上单调递增,∴当x=-1时,f(x)取最小值-1,当x=0时,f(x)取最大值0,
在[-1,0]上单调递增,∴当x=-1时,f(x)取最小值-1,当x=0时,f(x)取最大值0,
即{y|y=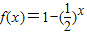 ,x∈[-1,0]}=[-1,0],故②中函数是一阶回归函数,故②正确;
,x∈[-1,0]}=[-1,0],故②中函数是一阶回归函数,故②正确;
∵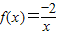 ,∴x∈(0,+∞)时,y=f(f(x))=
,∴x∈(0,+∞)时,y=f(f(x))=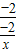 =x∈(0,+∞),即③中函数是二阶回归函数,故③正确;
=x∈(0,+∞),即③中函数是二阶回归函数,故③正确;
∵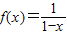 ,∴x∈(2,+∞)时,y=f(f(f(x)))=
,∴x∈(2,+∞)时,y=f(f(f(x)))=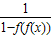 =
=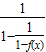 =
=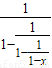 =
=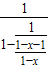 =
=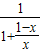 =
=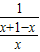 =x∈(2,+∞),即④中函数是三阶回归函数,故④正确;
=x∈(2,+∞),即④中函数是三阶回归函数,故④正确;
故选D
点评:X本题又命题的真假判断为载体,考查了基本函数的定义域,值域,单调性,其中正确理解新定义,是解答的关键.
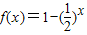 在[-1,0]上,是否满足定义可判断①②的真假;根据二阶回归函数的概念,判断
在[-1,0]上,是否满足定义可判断①②的真假;根据二阶回归函数的概念,判断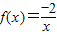 在(0,+∞)上是否满足定义可判断③的真假;根据三阶回归函数的概念,判断
在(0,+∞)上是否满足定义可判断③的真假;根据三阶回归函数的概念,判断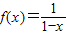 在(2,+∞)上是否满足定义可判断④的真假;
在(2,+∞)上是否满足定义可判断④的真假;解答:解:∵f(x)=3-x在[1,2]上单调递减,∴当x=1时,f(x)取最大值2,当x=2时,f(x)取最小值1,
即{y|y=f(x)=3-x,x∈[1,2]}=[1,2],故①中函数是一阶回归函数,故①正确;
∵
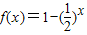 在[-1,0]上单调递增,∴当x=-1时,f(x)取最小值-1,当x=0时,f(x)取最大值0,
在[-1,0]上单调递增,∴当x=-1时,f(x)取最小值-1,当x=0时,f(x)取最大值0,即{y|y=
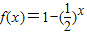 ,x∈[-1,0]}=[-1,0],故②中函数是一阶回归函数,故②正确;
,x∈[-1,0]}=[-1,0],故②中函数是一阶回归函数,故②正确;∵
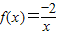 ,∴x∈(0,+∞)时,y=f(f(x))=
,∴x∈(0,+∞)时,y=f(f(x))=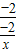 =x∈(0,+∞),即③中函数是二阶回归函数,故③正确;
=x∈(0,+∞),即③中函数是二阶回归函数,故③正确;∵
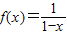 ,∴x∈(2,+∞)时,y=f(f(f(x)))=
,∴x∈(2,+∞)时,y=f(f(f(x)))=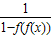 =
=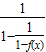 =
=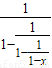 =
=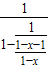 =
=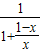 =
=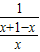 =x∈(2,+∞),即④中函数是三阶回归函数,故④正确;
=x∈(2,+∞),即④中函数是三阶回归函数,故④正确;故选D
点评:X本题又命题的真假判断为载体,考查了基本函数的定义域,值域,单调性,其中正确理解新定义,是解答的关键.

练习册系列答案
相关题目

 .请结合(I)中的结论证明x1<x3<x2.
.请结合(I)中的结论证明x1<x3<x2.
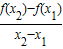 .请结合(I)中的结论证明x1<x3<x2.
.请结合(I)中的结论证明x1<x3<x2.