题目内容
如图，在正三角形ABC中，D、E、F分别为各边的中点，G、H、I分别为DE、FC、EF的中点，将△ABC沿DE、EF、FD折成三棱锥以后，BG与IH所成角的弧度数为 ( )
A.
B.
C.arccos
D.arccos
答案：A 【解析】考查异面直线所成角的求法,折叠后的图形如图所示：
因为I、H、G均为中点,所以IH∥AE所以∠GAE即为所求异面直线的夹角.由△ADE为正三角形得∠GAE=即为所求.
练习册系列答案
活力课时同步练习册系列答案
相关题目
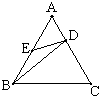如图，在正三角形ABC中，D、E分别在AC、AB上，| AD |
| AC |
| 1 |
| 3 |
| A、△AED∽△BED |
| B、△AED∽△CBD |
| C、△AED∽△ABD |
| D、△BAD∽△BCD |
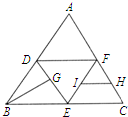如图，在正三角形ABC中，D，E，F分别为AB，BC，AC的中点，G，H，I分别为DE，FC，EF的中点，将
B．arccos
C．
D．arccos
