题目内容
如图,在正三角形ABC中, D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将△ABC沿DE,EF,DF折成三棱锥,则异面直线BG与IH所成的角为
A. | B.arccos | C. | D.arccos |
A
解析考点:异面直线及其所成的角;棱锥的结构特征.
分析:先画出折叠后的直观图画出来,再将两条异面直线平移到同一个平面内,最后在平面三角形中计算此角即可
解:将△ABC沿DE,EF,DF折成三棱锥如图 ,设顶点为P
,设顶点为P
由三角形中位线定理,IH∥PE,
∴∠EPG就是异面直线BG与IH所成的角
在三角形PED中,
∴∠DPG=∠EPG=
故选A

练习册系列答案
相关题目
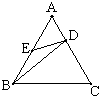 如图,在正三角形ABC中,D、E分别在AC、AB上,
如图,在正三角形ABC中,D、E分别在AC、AB上,| AD |
| AC |
| 1 |
| 3 |
| A、△AED∽△BED |
| B、△AED∽△CBD |
| C、△AED∽△ABD |
| D、△BAD∽△BCD |
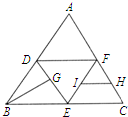 如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将
如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将
 B.arccos
B.arccos C.
C. D.arccos
D.arccos
