题目内容
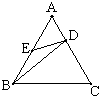如图，在正三角形ABC中，D、E分别在AC、AB上，| AD |
| AC |
| 1 |
| 3 |
| A、△AED∽△BED |
| B、△AED∽△CBD |
| C、△AED∽△ABD |
| D、△BAD∽△BCD |
分析：本题可以采用排除法，即根据已知中正三角形ABC中，D、E分别在AC、AB上，
=
，AE=BE，我们可以分别得到：△AED、△BCD为锐角三角形，△BED、△ABD为钝角三角形，然后根据锐角三角形不可能与钝角三角形相似排除错误答案，得到正确答案．
| AD |
| AC |
| 1 |
| 3 |
解答：解：由已知中正三角形ABC中，D、E分别在AC、AB上，
=
，AE=BE，
易判断出：△AED为一个锐角三角形，△BED为一个钝角三角形，故A错误；
△ABD也是一个钝角三角形，故C也错误；
但△BCD为一个锐角三角形，故D也错误；
故选B
| AD |
| AC |
| 1 |
| 3 |
易判断出：△AED为一个锐角三角形，△BED为一个钝角三角形，故A错误；
△ABD也是一个钝角三角形，故C也错误；
但△BCD为一个锐角三角形，故D也错误；
故选B
点评：本题考查的知识点是相似三角形的判定，其中在解答选择题时，我们可以直接根据相似三角形的定义，大小不同，形状相同，排除错误答案，得到正确结论．
练习册系列答案
阅读快车系列答案
相关题目
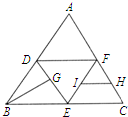如图，在正三角形ABC中，D，E，F分别为AB，BC，AC的中点，G，H，I分别为DE，FC，EF的中点，将
B．arccos
C．
D．arccos
