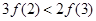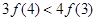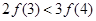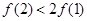题目内容
函数f(x)="xln" êxú的大致图象是 ( )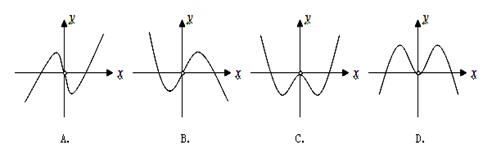
A
解析试题分析：∵函数f（x）=xln|x|，可得f（-x）=-f（x），f（x）是奇函数，其图象关于原点对称，排除C，D，又f′（x）=lnx+1，令f′（x）＞0得：x＞
，得出函数f（x）在（，+∞）上是增函数，排除B，故选A
考点：本题考查函数性质的应用、不等式的解法
点评：此类问题不仅考查学生的运算求解能力，还考查数形结合思想、化归与转化思想．属于基础题
练习册系列答案
相关题目
函数
的值域是（ ）
A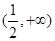． | B． | C． | D． |
已知定义在R上的函数
满足
，如图表示该函数在区间
上的图象，则
等于
| A．3 | B．2 | C．1 | D．0 |
如图，在平面直角坐标系中，正六边形
的中心在坐标原点，边长为
，
平行于
轴，直线
(
为常数)与正六边形交于
两点，记
的面积为
，则关于函数
的奇偶性的判断正确的是（ ）
| A．一定是奇函数 | B．—定是偶函数 |
| C．既不是奇函数，也不是偶函数 | D．奇偶性与有关 |
定义在R上的函数f(x)的图像关于x＝1对称，且当x≥1时，f(x)＝3x－1，则有( )
A．f <f < | B．f <f<f | C．f<f<f | D．f<f<f |
定义在R上的函数y=f（x）是增函数，且函数y=f（x－3）的图象关于点（3，0）成中心对称，若s，t满足f（s
－2s） ≥－f（2t－t），则
| A．s≥t | B．s<t | C．|s－1|≥|t－1| | D．s+t≥0 |
设函数
为定义在
上的奇函数，对任意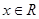
都有
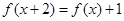成立，则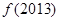
的值为（ ）
A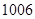． | B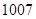． | C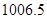． | D．无法确定 |
若2x－3－x≥2－y－3y，则
| A．x－y≥0 | B．x－y≤0 | C．x＋y≥0 | D．x＋y≤0 |
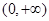上的单调递减函数
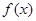，若
，则下列不等式成立的是（ ）
