题目内容
函数 的值域是( )
的值域是( )
A.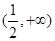 | B. | C. | D. |
C
解析试题分析:根据题意,由于函数 ,令
,令 ,那么函数y=
,那么函数y= ,
, ,那么结合二次函数的图像与性质,对称轴为t=-
,那么结合二次函数的图像与性质,对称轴为t=- ,可知函数的值域为
,可知函数的值域为
考点:函数的值域
点评:解决的关键是采用换元法思想来化为二次函数求解最值。属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数 有两个不同的零点,则实数
有两个不同的零点,则实数 的取值范围是
的取值范围是
A. | B. |
C.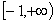 | D. |
为了得到函数 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( )
| A.向右平移1个单位再向上平移1个单位 |
| B.向左平移1个单位再向上平移1个单位 |
| C.向左平移1个单位再向下平移1个单位 |
| D.向右平移1个单位再向下平移1个单位 |
函数 的零点所在区间是( )
的零点所在区间是( )
A. | B.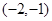  | C.(1,2) | D. |
函数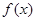 的定义域为开区间
的定义域为开区间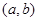 ,导函数
,导函数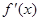 在
在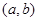 内的图象如图所示,则函数
内的图象如图所示,则函数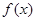 在开区间
在开区间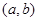 内有极大值( )
内有极大值( )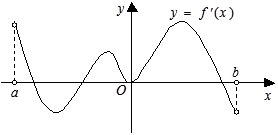
| A.1个 | B.4个 |
| C.3个 | D.2个 |
下列函数中,既是奇函数又在区间(0.+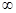 )上单调递增的函数是( )
)上单调递增的函数是( )
| A.y= 1nx | B.y=x3 | C.y=2| x| | D.y= sinx |
 和
和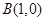 ,动点
,动点 在直线
在直线 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像是( )
的大致图像是( )
 在
在 上是增函数,则( )
上是增函数,则( ) >0 B
>0 B