题目内容
如图,在平面直角坐标系中,正六边形 的中心在坐标原点,边长为
的中心在坐标原点,边长为 ,
, 平行于
平行于 轴,直线
轴,直线 (
( 为常数)与正六边形交于
为常数)与正六边形交于 两点,记
两点,记 的面积为
的面积为 ,则关于函数
,则关于函数 的奇偶性的判断正确的是( )
的奇偶性的判断正确的是( )
| A.一定是奇函数 | B.—定是偶函数 |
| C.既不是奇函数,也不是偶函数 | D.奇偶性与 有关 有关 |
B
解析试题分析:设点 、
、 关于原点的对称点分别为为
关于原点的对称点分别为为 、
、 ,可知
,可知 、
、 在正六边形的边上.当直线
在正六边形的边上.当直线 在某一个确定的位置时,对应有一个
在某一个确定的位置时,对应有一个 的值,那么
的值,那么
易得直线 的斜率仍为
的斜率仍为 ,对应的截距为
,对应的截距为 ,显然
,显然 的面积与
的面积与
的面积相等,即函数 关于
关于 轴对称,所以
轴对称,所以 是偶函数.故选B.
是偶函数.故选B.
考点:函数奇偶性
点评:主要是考查了对数函数奇偶性的概念的运用,属于基础题。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
下列函数中,既是奇函数又在区间(0.+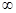 )上单调递增的函数是( )
)上单调递增的函数是( )
| A.y= 1nx | B.y=x3 | C.y=2| x| | D.y= sinx |
 在
在 上是增函数,则( )
上是增函数,则( ) >0 B
>0 B  的图象如图,那么导函数
的图象如图,那么导函数 的图象可能是( )
的图象可能是( )

 的一个根所在的区间是
的一个根所在的区间是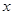
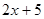
 B.
B.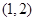 C.
C.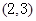 D.
D.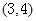
 ,观察:
,观察: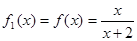 ,
,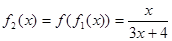 ,,
,, ,
, 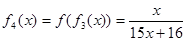 ……根据以上事实,由归纳推理可得当
……根据以上事实,由归纳推理可得当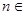 N*且
N*且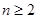 时,
时, 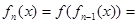 ( )
( )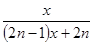
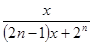
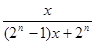
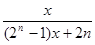
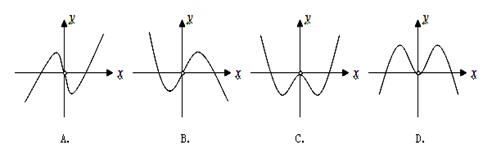
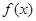 ,
,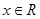 ,且
,且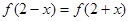 ,当
,当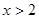 时,
时,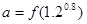 ,
,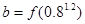 ,
,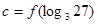 ,则
,则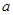 、
、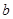 、
、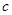 的大小顺序是( )。
的大小顺序是( )。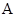 .
. 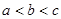
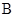 .
. 
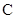 .
. 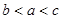
 .
. 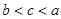
 的图象大致是
的图象大致是