题目内容
命题“?x∈R+,x>x2”的否定是
?x∈R+,使得x≤x2
?x∈R+,使得x≤x2
.分析:根据命题“?x∈R+,x>x2”是特称命题,其否定为全称命题,即?x∈R+,使得x≤x2,从而得到答案.
解答:解:∵命题“?x∈R+,x>x2”是特称命题
∴否定命题为:?x∈R+,使得x≤x2
故答案为:?x∈R+,使得x≤x2.
∴否定命题为:?x∈R+,使得x≤x2
故答案为:?x∈R+,使得x≤x2.
点评:这类问题的常见错误是没有把全称量词改为存在量词,或者对于“>”的否定用“<”了.这里就有注意量词的否定形式.如“都是”的否定是“不都是”,而不是“都不是”.特称命题的否定是全称命题,“存在”对应“任意”.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
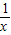 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )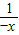 =-(x+
=-(x+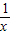 )=-f(x),∴f(x)是奇函数
)=-f(x),∴f(x)是奇函数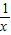 +(-x)+(-
+(-x)+(-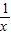 )=0,∴f(x)=-f(-x),∴f(x)是奇函数
)=0,∴f(x)=-f(-x),∴f(x)是奇函数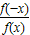 =
=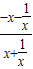 =-1,∴f(-x)=-f(x),∴f(x)是奇函数
=-1,∴f(-x)=-f(x),∴f(x)是奇函数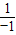 =-2,又f(1)=1+
=-2,又f(1)=1+ =2
=2