题目内容
给出如下几个结论：①命题“?x∈R，sinx+cosx=2”的否定是“?x∈R，sinx+cosx≠2”；②命题“?x∈R，sinx+
≥2”的否定是“?x∈R，sinx+
＜2”；③对于?x∈（0，
），tanx+
≥2；
④?x∈R，使sinx+cosx=
．其中正确的为（ ）
| 1 |
| sinx |
| 1 |
| sinx |
| π |
| 2 |
| 1 |
| tanx |
④?x∈R，使sinx+cosx=
| 2 |
| A、③ | B、③④ |
| C、②③④ | D、①②③④ |
分析：全称命题的否定是特称命题，特称命题的否定是全称命题，判断①②③的正误，利用基本不等式判断④的正误；
解答：解：根据全称命题的否定是特称命题，特称命题的否定是全称命题，可知①不正确；②正确；
由基本不等式可知③正确；由sinx+cosx=
sin（x+
）∈[-
，
]，可知④正确；
故选C．
由基本不等式可知③正确；由sinx+cosx=
| 2 |
| π |
| 4 |
| 2 |
| 2 |
故选C．
点评：本题是基础题，考查三角函数的最值，基本不等式的应用，考查分析问题解决问题的能力．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
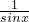≥2”的否定是“?x∈R，sinx+
），tanx+
≥2；
．其中正确的为
≥2”的否定是“?x∈R，sinx+
＜2”；③对于?x∈（0，
），tanx+
≥2；
．其中正确的为（ ）
≥2”的否定是“?x∈R，sinx+
＜2”；③对于?x∈（0，
），tanx+
≥2；
．其中正确的为（ ）
≥2”的否定是“?x∈R，sinx+
＜2”；③对于?x∈（0，
），tanx+
≥2；
．其中正确的为（ ）