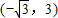题目内容
直线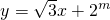 和圆x2+y2=n2相切,其中m、n∈N*,|m-n|≤5,试写出所有满足条件的有序实数对(m,n):________.
和圆x2+y2=n2相切,其中m、n∈N*,|m-n|≤5,试写出所有满足条件的有序实数对(m,n):________.
(1,1),(2,2),(3,4),(4,8)
分析:由直线和圆相切的性质可得,圆心到直线的距离等于半径,化简可得 2m=2n.
解答:∵直线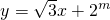 和圆x2+y2=n2相切,其中m、n∈N*,∴
和圆x2+y2=n2相切,其中m、n∈N*,∴ =n,
=n,
2m=2n,再由|m-n|≤5 可得:m=1,2,3,4时,满足条件.
满足条件的有序实数对(m,n)有:(1,1) (2,2),(3,4),(4,8),
故答案为:(1,1)、(2,2),(3,4),(4,8).
点评:本题考直线和圆的位置关系,查点到直线的距离公式的应用.
分析:由直线和圆相切的性质可得,圆心到直线的距离等于半径,化简可得 2m=2n.
解答:∵直线
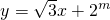 和圆x2+y2=n2相切,其中m、n∈N*,∴
和圆x2+y2=n2相切,其中m、n∈N*,∴ =n,
=n,2m=2n,再由|m-n|≤5 可得:m=1,2,3,4时,满足条件.
满足条件的有序实数对(m,n)有:(1,1) (2,2),(3,4),(4,8),
故答案为:(1,1)、(2,2),(3,4),(4,8).
点评:本题考直线和圆的位置关系,查点到直线的距离公式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和圆x2+y2=16交于A,B两点,则AB的中点坐标为( )
和圆x2+y2=16交于A,B两点,则AB的中点坐标为( )