题目内容
(本题满分13分)设数列 为单调递增的等差数列
为单调递增的等差数列 且
且 依次成等比数列.
依次成等比数列.
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)若 求数列
求数列 的前
的前 项和
项和 ;
;
(Ⅲ)若 ,求证:
,求证:
(1)
(2)
(3)根据 ,放缩来求和得到证明。
,放缩来求和得到证明。
解析试题分析:解:⑴ …3分
…3分
⑵
则 …7分
…7分
⑶
而
所以
 …………………….13分
…………………….13分
考点:本试题主要是考查了数列的通项公式的求解,以及数列求和的应用。
点评:解决该试题最重要的是第一步中通项公式的求解,利用等差数列的通项公式,得到数列 ,然后利用裂项求和得到第二问,裂项法是求和中重要而又常用 方法之一。同时能借助于放缩法得到不等式的证明。第三问是个难点。
,然后利用裂项求和得到第二问,裂项法是求和中重要而又常用 方法之一。同时能借助于放缩法得到不等式的证明。第三问是个难点。

练习册系列答案
相关题目
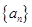 的前
的前 项和为
项和为 ,且
,且
 的递推关系式
的递推关系式 ,并求
,并求 ,
, ,
, 的值;
的值;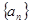 满足
满足 .
. ,证明:数列
,证明:数列 为等差数列,并求数列
为等差数列,并求数列 项和
项和 .
. 的首项为
的首项为 ,
, 时,
时, ,数列
,数列 对任意
对任意 均有
均有
 ,数列
,数列 满足
满足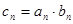 ,记数列
,记数列 项和为
项和为 ,求证
,求证 .
. 同时满足:①不等式
同时满足:①不等式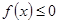 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在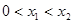 ,使得不等式
,使得不等式 成立.
成立.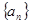 的前
的前 项和
项和 ,
, 中,令
中,令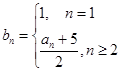 ,
,
 ,求
,求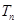 ;
;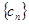 中,所有满足
中,所有满足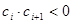 的正整数
的正整数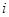 的个数称为这个数列
的个数称为这个数列 (
( ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数 ,公比为正整数
,公比为正整数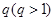 的无穷等比数列
的无穷等比数列 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项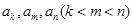 .
.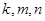 之间满足的等量关系;
之间满足的等量关系; 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了 与
与 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确; 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.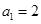 ,点
,点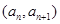 在函数
在函数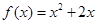 的图象上,其中
的图象上,其中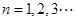
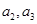 ;
;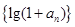 是等比数列;
是等比数列;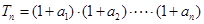 ,求
,求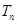 及数列
及数列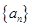 的通项
的通项 的前
的前 项和为
项和为 ,
, ,
, ,等差数列
,等差数列 满足
满足 ,
, ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 满足
满足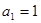 ,
,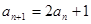 (
(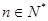 ).
). 满足
满足 (
(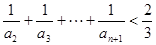 (
(