题目内容
已知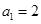 ,点
,点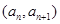 在函数
在函数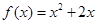 的图象上,其中
的图象上,其中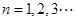
(1)求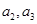 ;
;
(2)证明数列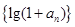 是等比数列;
是等比数列;
(3)设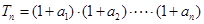 ,求
,求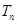 及数列
及数列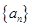 的通项
的通项
(1) ;(2)由已知
;(2)由已知 ,
,  ,
,
 ,两边取对数得
,两边取对数得 ,即
,即
;(3)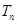 =
= ;
;
解析试题分析:(1)
(2)由已知 ,
, 

 ,两边取对数得
,两边取对数得 ,即
,即
 是公比为2的等比数列.
是公比为2的等比数列.
(3)由(2)知

 (*)
(*)

 =
=
由(*)式得
考点:本题考查了数列通项公式的求法及其前n项问题
点评:解决数列的前n项和的方法一般有:公式法、倒序相加法、错位相减法、分组求和法、裂项法等,要求学生掌握几种常见的裂项比如

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 的前
的前 项和
项和 ,数列
,数列 满足
满足
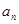 ;(2)求数列
;(2)求数列 ;
; 恒成立
恒成立 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
, 为其前
为其前 项和,且满足
项和,且满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 和数列
和数列 的前n项和
的前n项和 ;
; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 为单调递增的等差数列
为单调递增的等差数列 且
且 依次成等比数列.
依次成等比数列. ;
; 求数列
求数列 的前
的前 项和
项和 ;
; ,求证:
,求证:
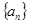 是递增数列,且满足
是递增数列,且满足 。
。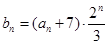 ,求数列
,求数列 的前
的前 项和
项和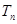 。
。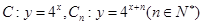 ,从
,从 上的点
上的点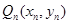 作
作 轴的垂线,交
轴的垂线,交 于点
于点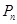 ,再从点
,再从点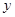 轴的垂线,交
轴的垂线,交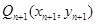 ,
,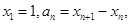
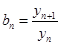 .。
.。 求数列
求数列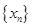 的通项公式;
的通项公式;  记
记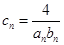 ,数列
,数列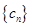 的前
的前 项和为
项和为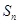 ,试比较
,试比较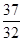 的大小
的大小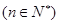 ;
;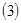 记
记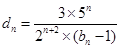 ,数列
,数列 的前
的前 ,试证明:
,试证明: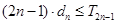 。
。 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 ,
, .
. ,
, 为数列
为数列 的前
的前 满足
满足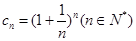 ,试证明:
,试证明: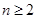 时,有
时,有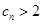 ;
;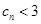 .
.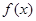 定义在区间
定义在区间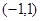 上,
上,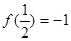 ,且当
,且当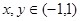 时,
时,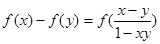 .又数列
.又数列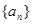 满足
满足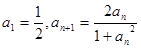 .
. 的表达式;
的表达式;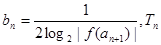 为数列
为数列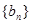 的前
的前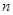 项和,若
项和,若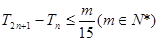 对
对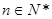 恒成立,求
恒成立,求 的最小值.
的最小值.