题目内容
(2012•珠海一模)已知函数f(x)=x3-ax2+2x,x∈R
(1)求f(x)的单调区间;
(2)若x∈(2,+∞)时,f(x)>
x恒成立,求实数a的取值范围.
(1)求f(x)的单调区间;
(2)若x∈(2,+∞)时,f(x)>
| 1 | 2 |
分析:(1)求导函数,利用根的判别式,结合导数的正负,可得f(x)的单调区间;
(2)x∈(2,+∞)时,f(x)>
x恒成立,等价于x∈(2,+∞)时,x+
>a,求出左边对应函数的最值,即可求实数a的取值范围.
(2)x∈(2,+∞)时,f(x)>
| 1 |
| 2 |
| 3 |
| 2x |
解答:解:(1)f′(x)=3x2-2ax+2,△=(-2a)2-4×3×2=4a2-24
①当△≥0,即a≤-
或a≥
时,f(x)在R上为增函数
②当△<0,即-
<a<
时,f′(x)=3x2-2ax+2有两个零点x1,x2,
且x1=
,x2=
此时f(x)的单调增区间为:(-∞,
),(
,+∞)
单调减区间为:(
,
)
(2)x∈(2,+∞)时,f(x)>
x恒成立,等价于x∈(2,+∞)时,x3-ax2+2x>
x恒成立,等价于x∈(2,+∞)时,x3+
x>ax2恒成立,等价于x∈(2,+∞)时,x+
>a,
令g(x)=x+
,则g′(x)=1-
,x∈(2,+∞)时,g′(x)>0,g(x)单调递增,
故x∈(2,+∞),g(x)>g(2)=
,所以a≤
.
①当△≥0,即a≤-
| 6 |
| 6 |
②当△<0,即-
| 6 |
| 6 |
且x1=
a-
| ||
| 3 |
a+
| ||
| 3 |
此时f(x)的单调增区间为:(-∞,
a-
| ||
| 3 |
a+
| ||
| 3 |
单调减区间为:(
a-
| ||
| 3 |
a+
| ||
| 3 |
(2)x∈(2,+∞)时,f(x)>
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2x |
令g(x)=x+
| 3 |
| 2x |
| 3 |
| 2x2 |
故x∈(2,+∞),g(x)>g(2)=
| 7 |
| 4 |
| 7 |
| 4 |
点评:本题考查函数的单调性,考查导数知识的运用,考查恒成立问题,考查函数的最值,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
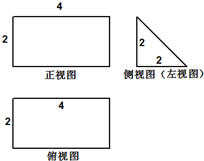 (2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( )
(2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( ) (2012•珠海一模)如图,在△ABC中,已知
(2012•珠海一模)如图,在△ABC中,已知