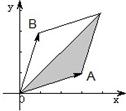
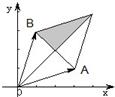
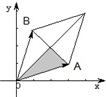
题目内容
设向量| OA |
| 3 |
| OB |
| π |
| 2 |
(1)若|
| AB |
| 13 |
(2)求△AOB面积的最大值.
分析:(1)先利用向量的减法求出
,在代入向量的模长计算公式整理即可求出tanθ的值;
(2)先利用θ的范围求出∠AOB,在代入三角形面积计算公式,利用θ的取值范围,即可求出△AOB面积的最大值.
| AB |
(2)先利用θ的范围求出∠AOB,在代入三角形面积计算公式,利用θ的取值范围,即可求出△AOB面积的最大值.
解答:解:(1):依题意得,
=
-
=(cosθ-3,sinθ+
),…(2分)
所以|
|2=(cosθ-3)2+(sinθ+
)2=13-6cosθ+2
sinθ=13,…(4分)
所以
sinθ=3cosθ.因为cosθ≠0,所以tanθ=
.…(7分)
(2):由0≤θ≤
,得∠AOB=θ+
.…(9分)
所以S△AOB=
|
||
|sin∠AOB=
×2
×1×sin(θ+
)=
sin(θ+
)…(12分)
所以当θ=
时,△AOB的面积取得最大值
.…(14分)
| AB |
| OB |
| OA |
| 3 |
所以|
| AB |
| 3 |
| 3 |
所以
| 3 |
| 3 |
(2):由0≤θ≤
| π |
| 2 |
| π |
| 6 |
所以S△AOB=
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
所以当θ=
| π |
| 3 |
| 3 |
点评:本题主要考查平面向量的综合知识.解决第二问的关键是会用三角形的面积计算公式,且注意考虑角的范围.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目