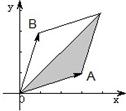
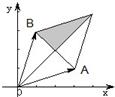
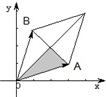
题目内容

设向量
OA
=（3，1），
OB
=（-1，2），向量
OC
⊥
OB
，
BC
∥
OA
，又
OD
+
OA
=
OC
，求
OD
．
分析：设
OC
=（x，y），由
OC
•
OB
=0和
BC
∥
OA
，建立方程组解出x，y，再由
OD
=
OC
-
OA
 求得
OD
的坐标．
解答：解：设
OC
=（x，y），∵
OC
⊥
OB
，∴
OC
•
OB
=0，∴2y-x=0，①
又∵
BC
∥
OA
，
BC
=（x+1，y-2），∴3（y-2）-（x+1）=0，
即3y-x-7=0，②由①，②解得   x=14，y=7，∴
OC
=（14，7），
则
OD
=
OC
-
OA
=（11，6）．
点评：本题考查两个向量垂直、平行的性质，两个向量 坐标形式的运算法则的应用．
练习册系列答案
相关题目
平面直角坐标系中，O为坐标原点，设向量
OA
=
a
，
OB
=
b
，其中
a
=(3，1)，
b
=(1，3)，若
OC
=λ
a
+μ
b
，且0≤μ≤λ≤1，那么C点所有可能的位置区域用阴影表示正确的是（　　）
A、精英家教网
B、精英家教网
C、精英家教网
D、精英家教网
设向量
OA
=(3，-
3
)，
OB
=(cosθ，sinθ)，其中0≤θ≤
π
2
．
（1）若|
AB
|=
13
，求tanθ的值；
（2）求△AOB面积的最大值．
（1）|
a
|=3，|
b
|=4，且（
a
+2
b
）•（
a
-3
b
）=-93，求向量
a
与
b
的夹角＜
a
，
b
＞；
（2）设向量
OA
=（-1，-2），
OB
=（1，4），
OC
=（2，-4），在向量
OC
上是否存在点P，使得
PA
⊥
PB
，若存在，求出点P的坐标，若不存在，请说明理由．
设向量
OA
=（3，1），
OB
=（-1，2），向量
OC
⊥
OB
，
BC
∥
OA
，又
OD
+
OA
=
OC
，求
OD
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网