题目内容
【题目】【2018届福建省福州市高三上学期期末】过椭圆![]() 的右焦点作
的右焦点作![]() 轴的垂线,交
轴的垂线,交![]() 于
于![]() 两点,直线
两点,直线![]() 过
过![]() 的左焦点和上顶点.若以
的左焦点和上顶点.若以![]() 为直径的圆与
为直径的圆与![]() 存在公共点,则
存在公共点,则![]() 的离心率的取值范围是( )
的离心率的取值范围是( )
A. 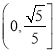 B.
B. 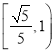 C.
C. 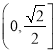 D.
D. 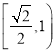
【答案】A
【解析】直线![]() 的方程为
的方程为![]() ,圆心坐标为
,圆心坐标为![]() ,半径为
,半径为![]() 与圆有公共点,
与圆有公共点,  ,可得
,可得![]() ,
, ![]() ,
, ![]() ,故选A.
,故选A.
【方法点晴】本题主要考查利用椭圆的简单性质及求椭圆的离心率范围,属于难题. 求解与双曲线性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.求离心率范围问题应先将 ![]() 用有关的一些量表示出来,再利用其中的一些关系构造出关于
用有关的一些量表示出来,再利用其中的一些关系构造出关于![]() 的不等式,从而求出
的不等式,从而求出![]() 的范围 . 本题是利用点到直线的距离小于圆半径构造出关于
的范围 . 本题是利用点到直线的距离小于圆半径构造出关于![]() 的不等式,最后解出
的不等式,最后解出![]() 的范围.
的范围.

练习册系列答案
相关题目
【题目】已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.