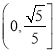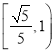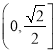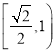题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数)
为参数)
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与圆
与圆![]() 相较于
相较于![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() ,
, ![]() ;(2)
;(2) ![]()
【解析】试题分析:(1)先根据圆心与半径写出圆标准方程,根据加减消元法得直线![]() 的直角坐标系,再根据
的直角坐标系,再根据![]() 将直角坐标方程化为极坐标方程(2)先化P点极坐标为直角坐标,再将直线参数方程代入圆直角坐标方程,利用韦达定理以及直线参数几何意义求
将直角坐标方程化为极坐标方程(2)先化P点极坐标为直角坐标,再将直线参数方程代入圆直角坐标方程,利用韦达定理以及直线参数几何意义求![]() 的值.
的值.
试题解析:圆![]() 的直角坐标方程为
的直角坐标方程为![]()
![]() 代入圆
代入圆![]() 得:
得: ![]()
化简得圆![]() 的极坐标方程:
的极坐标方程:![]()
由![]() 得
得![]() ∴
∴![]() 的极坐标方程为
的极坐标方程为![]()
(2)由![]() 得点
得点![]() 的直角坐标为
的直角坐标为![]()
∴直线![]() 的参数的标准方程可写成
的参数的标准方程可写成 (
(![]() 为参数)
为参数)
代入圆![]() 得:
得: 
化简得: ![]()
 ∴
∴![]()
∴![]()

练习册系列答案
相关题目
【题目】2018年1月8日,中共中央国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当![]() 时,y是x的二次函数;当
时,y是x的二次函数;当![]() 时,
时,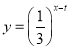 测得数据如下表(部分):
测得数据如下表(部分):
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式![]() ;
;
(2)当该产品中的新材料含量x为何值时,产品的性能指标值最大.