题目内容
已知抛物线![]() 的焦点F以及椭圆
的焦点F以及椭圆![]() (
(![]()
![]() )的上、下焦点及左、右顶点均在圆O:
)的上、下焦点及左、右顶点均在圆O:![]() 上。
上。
(1)求抛物线![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(2)过点F的直线交抛物线![]() 于A,B两不同点,交y轴于点N,已知
于A,B两不同点,交y轴于点N,已知![]() ,则
,则![]() 是否为定值?若是,求出其值;若不是,说明理由。
是否为定值?若是,求出其值;若不是,说明理由。
解析:(1)![]() ;(2)-1
;(2)-1
试题分析:(1)根据抛物线的焦点坐标满足圆的方程确定等量关系,求解抛物线方程;根据椭圆的焦点和右定点也在圆上,确定椭圆方程;(2)利用已知的向量关系式进行坐标转化求出![]() ,然后通过直线与抛物线方程联立,借助韦达定理进行化简
,然后通过直线与抛物线方程联立,借助韦达定理进行化简![]() 并求值。
并求值。
试题解析:(1)由抛物线![]() 的焦点
的焦点![]() 在圆O:
在圆O:![]() 上得:
上得:![]() 抛物线
抛物线![]()
同理由椭圆![]() 的上、下焦点
的上、下焦点![]() 及左、右顶点
及左、右顶点![]() 均在圆O:
均在圆O:![]() 上可解得:
上可解得:![]() 。
。
得椭圆![]() 。
。
(2)![]() 是定值,且定值为-1。
是定值,且定值为-1。
设直线AB的方程为![]() ,则
,则![]() 。
。
联立方程组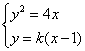 ,消去y得:
,消去y得:![]() ,
,
![]() ,且
,且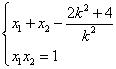 ,
,
由![]() 得:
得:![]() ,
,
整理得:![]() ,
,
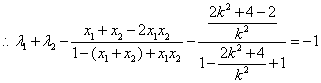

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
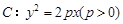 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设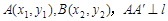 于
于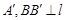 于
于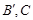 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②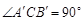 ;
; 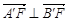 ; ④
; ④ ; ⑤.
; ⑤.
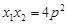
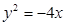 的焦点为F,其准线与x轴交于点
的焦点为F,其准线与x轴交于点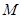 ,过点
,过点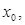 0)。
0)。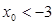 ;
;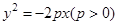 的焦点为F,过F的直线交y轴正半轴于点,交抛物线于A,B两点,其中A在第二象限。
的焦点为F,过F的直线交y轴正半轴于点,交抛物线于A,B两点,其中A在第二象限。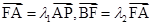 ,求
,求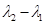 的值.
的值.