题目内容
在三棱锥A-BCD中,所有棱长都相等,过点A作底面BCD的垂线,垂足为H,点M是AH的中点,则∠BMC= .
考点:直线与平面垂直的性质
专题:数形结合,空间位置关系与距离
分析:根据已知先求得BH的长,从而可求MH,BM,CM的值,由勾股定理可得BC2=MB2+CM2,可得BM⊥MC,即可求得∠BMC的值.
解答:

解:设三棱锥A-BCD中,棱长为1,如图,在底面BCD中,连接BH交CD于F点,连接CH交BD于E点,
根据正三棱锥的特征,则△BEH∽△BFD,有
=
,即
=
,可得BH=
=
,
∴AH=
=
∴MH=
AH=
∴BM=
=
同理可证,CM=
=
BC=1
∴BC2=MB2+CM2=1
∴BM⊥MC
∴则∠BMC=
.


解:设三棱锥A-BCD中,棱长为1,如图,在底面BCD中,连接BH交CD于F点,连接CH交BD于E点,
根据正三棱锥的特征,则△BEH∽△BFD,有
| BH |
| BD |
| BE |
| BF |
| BH |
| 1 |
| ||||
|
| ||||
|
| ||
| 3 |
∴AH=
| AB2-BH2 |
| ||
| 3 |
∴MH=
| 1 |
| 2 |
| ||
| 6 |
∴BM=
| BH2+MH2 |
| ||
| 2 |
同理可证,CM=
| CH2+MH2 |
| ||
| 2 |
BC=1
∴BC2=MB2+CM2=1
∴BM⊥MC
∴则∠BMC=
| π |
| 2 |

点评:本题主要考查了直线与平面垂直的性质,正确的作出图形,分析边角关系是关键,属于基本知识的考查.

练习册系列答案
相关题目
若正n边形的两条对角线都与直线l垂直,则直线l一定垂直于这个正n边形所在的平面,则n的取值可能是( )
| A、8 | B、7 | C、6 | D、5 |
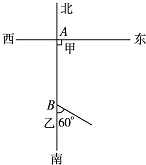 如图,A,B 两个小岛相距21海里,B 岛在 A 岛的正南方,现在甲船从 A 岛出发,以9海里/时的速度向 B 岛行驶,而乙船同时以6海里/时的速度离开 B 岛向南偏东60°方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.
如图,A,B 两个小岛相距21海里,B 岛在 A 岛的正南方,现在甲船从 A 岛出发,以9海里/时的速度向 B 岛行驶,而乙船同时以6海里/时的速度离开 B 岛向南偏东60°方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.