题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() ).下面表格所确定的点
).下面表格所确定的点![]() 中,恰有三个点在椭圆
中,恰有三个点在椭圆![]() 上.
上.
|
|
| 1 |
|
|
| 0 |
|
|
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为坐标原点,点
为坐标原点,点![]() ,
,![]() 分别为
分别为![]() 的上下顶点,直线
的上下顶点,直线![]() 经过
经过![]() 的右顶点
的右顶点![]() ,且与
,且与![]() 的另一个公共点为
的另一个公共点为![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() 与
与![]() 轴的交点
轴的交点![]() 异于
异于![]() ,
,![]() ,证明
,证明![]() 为定值.
为定值.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)点![]() 和点
和点![]() 关于原点对称,此两点必在椭圆上,故有
关于原点对称,此两点必在椭圆上,故有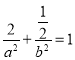 ,将剩余两个点的坐标代入椭圆方程
,将剩余两个点的坐标代入椭圆方程![]() 可得关于a与b的方程,与上式联立通过判断解的情况即可判断出那个点在椭圆上,进而求出方程;
可得关于a与b的方程,与上式联立通过判断解的情况即可判断出那个点在椭圆上,进而求出方程;
(2)设直线l的方程为:![]() ,由题易得
,由题易得![]() ,联立直线l与椭圆E的方程得:
,联立直线l与椭圆E的方程得:![]() ,由韦达定理得到
,由韦达定理得到![]() 和
和![]() 的表达式,
的表达式,
设点![]() ,直线AC的方程为:
,直线AC的方程为:![]() ,直线BD的方程为:
,直线BD的方程为:![]() ,
,
联立直线AC的方程和直线BD的方程得到点N的坐标,进而求出向量![]() ,
,
而![]() ,即可证明
,即可证明![]() 为定值.
为定值.
(1)点![]() 和点
和点![]() 关于原点对称,此两点必在椭圆上,
关于原点对称,此两点必在椭圆上,
故有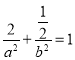 ①,
①,
将点![]() 代入
代入![]() 中得,
中得,![]() ,解得:
,解得:![]() ,
,
再将![]() 代入①中得:
代入①中得: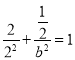 ,解得:
,解得:![]() ;
;
再将点![]() 代入
代入![]() 中得,
中得,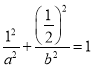 ②,联立①②得:
②,联立①②得: ,显然无解;
,显然无解;
综上,![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 的方程为:
的方程为:![]() ;
;
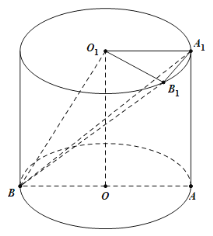
(2)由题意作图如下:
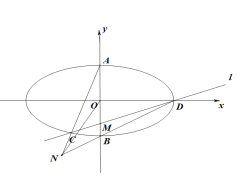
设直线l的方程为:![]() ,由条件知:
,由条件知:![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,
,
则点![]() ,向量
,向量![]() ,
,
设点![]() ,
,
联立直线l与椭圆E的方程,消去y得:![]() ,
,
所以![]() ,
,
直线AC的方程为:![]() ③,
③,
直线BD的方程为:![]() ④,
④,
设点![]() ,由③④,得:
,由③④,得: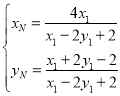 ,
,
又点![]() 在直线l上,所以:
在直线l上,所以:
![]()
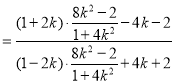
![]() ,
,
则向量![]() ,
,
所以![]() ,
,
故![]() 为定值
为定值![]() .
.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)司机师傅小李准备在一辆开了![]() 年的
年的![]() 型车和一辆开了
型车和一辆开了![]() 年的
年的![]() 型车中选择,为了尽最大可能实现
型车中选择,为了尽最大可能实现![]() 年内(含
年内(含![]() 年)不换车,试通过计算说明,他应如何选择.
年)不换车,试通过计算说明,他应如何选择.
附: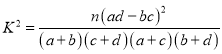 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |