��Ŀ����
����Ŀ��ijͬѧ��һ���о���ѧϰ�з��֣��������ʽ�ӵ�ֵ������ͬһ��������
1��sin213��+cos217�㩁sin13��cos17��
2��sin215��+cos215�㩁sin15��cos15��
3��sin218��+cos212�㩁sin18��cos12��
4��sin2����18�㣩+cos248�㩁sin2����18�㣩cos48��
5��sin2����25�㣩+cos255�㩁sin2����25�㣩cos55��
�����Դ��������ʽ����ѡ��һ����������������
�����ݣ��ļ�����������ͬѧ�ķ����ƹ�Ϊ���Ǻ��ʽ����֤����Ľ��ۣ�
���𰸡��⣺ѡ��2�����������£�
sin215��+cos215�㩁sin15��cos15��=1�� ![]() sin30��=
sin30��= ![]() ���� �������Ϊ
���� �������Ϊ ![]() ��
��
�����ݣ��ļ�����������ͬѧ�ķ����ƹ㣬�õ����Ǻ��ʽsin2��+cos2��30�㩁������sin��cos��30�㩁����= ![]() ��
��
֤����������һ��sin2��+cos2��30�㩁������sin��cos��30�㩁����=sin2��+ 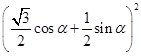 ��sin����cos30��cos��+sin30��sin����
��sin����cos30��cos��+sin30��sin����
=sin2��+ ![]() cos2��+
cos2��+ ![]() sin2��+
sin2��+ ![]() sin��cos����
sin��cos���� ![]() sin��cos����
sin��cos���� ![]() sin2��=
sin2��= ![]() sin2��+
sin2��+ ![]() cos2��=
cos2��= ![]() ��
��
����������sin2��+cos2��30�㩁������sin��cos��30�㩁����= ![]() +
+ ![]() ��sin����cos30��cos��+sin30��sin����
��sin����cos30��cos��+sin30��sin����
=1�� ![]() +
+ ![]() ��cos60��cos2��+sin60��sin2������
��cos60��cos2��+sin60��sin2������ ![]() sin2����
sin2���� ![]() sin2��
sin2��
=1�� ![]() +
+ ![]() cos2��+
cos2��+ ![]() sin2����
sin2���� ![]() sin2����
sin2���� ![]() =1��
=1�� ![]() ��
�� ![]() +
+ ![]() =
= ![]() ��
��
������������ѡ��2������sin215��+cos215�㩁sin15��cos15��=1�� ![]() sin30��=
sin30��= ![]() ���ɵ����������ֵ��
���ɵ����������ֵ��
�����ƹ㣬�õ����Ǻ��ʽsin2��+cos2��30�㩁������sin��cos��30�㩁����= ![]() ��֤������һ��ֱ���������Dz�����ҹ�ʽ�����ʽ����ߣ�����ɵý����
��֤������һ��ֱ���������Dz�����ҹ�ʽ�����ʽ����ߣ�����ɵý����
֤�������������ð�ǹ�ʽ�����Dz�����ҹ�ʽ��Ҫ���ʽ�ӻ�Ϊ ![]() +
+ ![]() ��sin����cos30��cos��+sin30��sin�������� 1��
��sin����cos30��cos��+sin30��sin�������� 1�� ![]() +
+ ![]() cos2��+
cos2��+ ![]() sin2��
sin2��
�� ![]() sin2����
sin2���� ![]() ������ɵý��
������ɵý��

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�