Question

已知某几何体的三视图如右图所示，其中俯视图为正三角形,设D为AA₁的中点.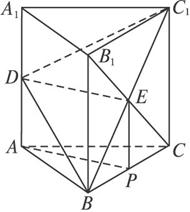

（1）作出该几何体的直观图并求其体积.

（2）求证：平面BB₁C₁C⊥平面BDC₁.

（3）BC边上是否存在点P，使AP∥平面BDC₁？若不存在，说明理由；若存在，证明你的结论.

Answer 1

（1）解：由题意可知该几何体为直三棱柱，且它的直观图如图所示.

∵几何体的底面积S=,高h=3,

∴所求体积V=3.

（2）证明：连结B₁C交BC₁于E点，则E为BC₁、B₁C的中点，连结DE.

∵AD=A₁D，AB=A₁C₁，∠BAD=∠DA₁C₁=90°,

∴△ABD≌△DA₁C₁.∴BD=DC₁.

∴DE⊥BC₁.

同理,DE⊥B₁C.

又∵B₁C∩BC₁=E，∴DE⊥面BB₁C₁C.

又∵DE面BDC₁，∴面BDC₁⊥面BB₁C₁C.

（3）解：取BC的中点P，连结AP，则AP∥平面BDC₁.

证明：连结PE，则PE平行且等于AD，

∴四边形APED为平行四边形.∴AP∥DE.

又DE平面BDC₁，AP平面BDC₁，

∴AP∥平面BDC₁.