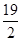题目内容
 如图,矩形纸片ABCD的边AB=24,AD=25,点E、F分别在边AB与BC上.现将纸片的右下角沿EF翻折,使得顶点B翻折后的新位置B1恰好落在边AD上.设
如图,矩形纸片ABCD的边AB=24,AD=25,点E、F分别在边AB与BC上.现将纸片的右下角沿EF翻折,使得顶点B翻折后的新位置B1恰好落在边AD上.设| BE | EF |
(1)函数f(t)的解析式;
(2)函数f(t)的定义域.
分析:(1)先设∠BFE=θ,则t=sinθ.根据边、角之间的关系得到:lsinθ+lsinθcos2θ=24,由此解得l=
=
=
=
.即可;
(2)从两个方面考虑:一方面,当点E与点A重合时,θ取最大值为
,t=sinθ取最大值为
;另一方面,当点E向右运动时,BE长度变小,为保持点B1在边AD上,则点F要向上运动,当点F与点C重合时,sinθ取得最小值.从而求得函数f(t)的定义域.
| 24 |
| sinθ+sinθcos2θ |
| 24 |
| sinθ(1+cos2θ) |
| 24 |
| sinθ(2-2sin2θ) |
| 12 |
| sinθ(1-sin2θ) |
(2)从两个方面考虑:一方面,当点E与点A重合时,θ取最大值为
| π |
| 4 |
| ||
| 2 |
解答:解:(1)设∠BFE=θ,则t=sinθ.
由于∠B1FE=∠BFE=θ,∠FB1E=∠FBE=
,
则∠AB1E=π-2θ-
=
-2θ,即∠AEB1=2θ.
而BE=lsinθ,AE=B1Ecos2θ=lsinθcos2θ,AE+BE=AB=24,
所以lsinθ+lsinθcos2θ=24,
解得l=
=
=
=
.
故l=f(t)=
.
(2)一方面,当点E与点A重合时,θ取最大值为
,t=sinθ取最大值为
..(10分)
另一方面,当点E向右运动时,BE长度变小,为保持点B1在边AD上,则点F要向上运动,
当点F与点C重合时,sinθ取得最小值.
又当点F与点C重合时,有25tanθ+25tanθcos2θ=24,
化简得,sinθ•cosθ=
,结合sin2θ+cos2θ=1,0<θ<
,解之得sinθ=
.
所以sinθ∈[
,
],从而,函数f(t)的定义域为t∈[
,
].
由于∠B1FE=∠BFE=θ,∠FB1E=∠FBE=
| π |
| 2 |
则∠AB1E=π-2θ-
| π |
| 2 |
| π |
| 2 |
而BE=lsinθ,AE=B1Ecos2θ=lsinθcos2θ,AE+BE=AB=24,
所以lsinθ+lsinθcos2θ=24,
解得l=
| 24 |
| sinθ+sinθcos2θ |
| 24 |
| sinθ(1+cos2θ) |
| 24 |
| sinθ(2-2sin2θ) |
| 12 |
| sinθ(1-sin2θ) |
故l=f(t)=
| 12 |
| t-t3 |
(2)一方面,当点E与点A重合时,θ取最大值为
| π |
| 4 |
| ||
| 2 |
另一方面,当点E向右运动时,BE长度变小,为保持点B1在边AD上,则点F要向上运动,
当点F与点C重合时,sinθ取得最小值.
又当点F与点C重合时,有25tanθ+25tanθcos2θ=24,
化简得,sinθ•cosθ=
| 12 |
| 25 |
| π |
| 4 |
| 3 |
| 5 |
所以sinθ∈[
| 3 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| ||
| 2 |
点评:在求实际问题对应的函数的解析式,我们一定要进一步分析自变量的取值范围,这不仅是为了让函数的解析式更准确,而且为利用函数的解析式求函数的值域,最值、单调性、奇偶性等打好基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系中,矩形纸片ABCD的长为2,宽为1.点A与坐标原点重合,AB,AD边分别在x轴、y轴的正半轴上.将矩形纸片沿直线折叠一次,使点A落在边CD上,记为点A′.
如图,在平面直角坐标系中,矩形纸片ABCD的长为2,宽为1.点A与坐标原点重合,AB,AD边分别在x轴、y轴的正半轴上.将矩形纸片沿直线折叠一次,使点A落在边CD上,记为点A′.
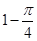 B.
B. C.
C.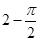 D.
D.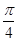

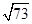 B.9 C.
B.9 C.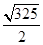 D.
D.