题目内容
12.已知函数f(x)为偶函数,且f(x)=x2-$\frac{1}{x}$(x>0),则f′(-1)=-3.分析 设x<0,则-x>0.由于f(x)=x2-$\frac{1}{x}$(x>0),可得f(-x)=x2+$\frac{1}{x}$.因此f(x)=x2+$\frac{1}{x}$.利用导数的运算法则即可得出.
解答 解:∵设x<0,则-x>0.
∵f(x)=x2-$\frac{1}{x}$(x>0),
∴f(-x)=x2+$\frac{1}{x}$.
∴f(x)=x2+$\frac{1}{x}$.
f′(x)=2x-$\frac{1}{{x}^{2}}$,
则f′(-1)=-2-1=-3.
故答案为:-3.
点评 本题考查了导数的运算法则、函数的奇偶性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知p,q为命题,则“p∨q为假”是“p∧q为假”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知函数f(x)是定义域为R的偶函数,且f(x+1)=$\frac{1}{f(x)}$,若f(x)在[-1,0]上是减函数,记a=f(log0.52),b=f(log24),c=f(20.5),则( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
1.若将函数f(x)=cosx(sinx+cosx)-$\frac{1}{2}$的图象向右平移φ个单位,所得函数是奇函数,则φ的最小正值是( )
| A. | $\frac{3π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
 如图,四棱锥O-ABCD中,AC垂直平分BD,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OD}$|=1,则($\overrightarrow{OA}$+$\overrightarrow{OC}$)•($\overrightarrow{OB}$-$\overrightarrow{OD}$)的值是3.
如图,四棱锥O-ABCD中,AC垂直平分BD,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OD}$|=1,则($\overrightarrow{OA}$+$\overrightarrow{OC}$)•($\overrightarrow{OB}$-$\overrightarrow{OD}$)的值是3.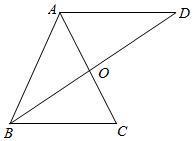 如图,在△ABC中,AB=AC=3,BC=2,B的角平分线交过点A且与BC平行的直线于D,AC与BD交于点O.
如图,在△ABC中,AB=AC=3,BC=2,B的角平分线交过点A且与BC平行的直线于D,AC与BD交于点O.