Question

校园内计划修建一个矩形花坛，并在花坛内装置两个相同的喷水器，已知喷水器的喷水区域是半径为5 m的圆.问如何设计花坛的尺寸和两个喷水器的位置，才能使花坛的面积最大且能全部喷到水？

Answer 1

解：设花坛的长、宽分别为x m、y m，根据设计要求，矩形花坛应在喷水区域内，且顶点应恰好位于喷水区域的边界(如图)，依题得()²+()²=25.

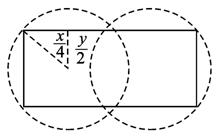
    问题转化为在x＞0,y＞0,+y²=100的条件下求S=xy的最大值.

方法一：∵S=xy=2··y≤()²+y²=100,由=y，+y²=100及x、y＞0,得

x=10,y=5,S_max=100.

方法二：依题意令x=20cosθ,

y=10sinθ(0＜θ＜),

    则S=xy=200sinθcosθ=100sin2θ≤100,

    解得θ=,x=10,y=5,S_max=100.

方法三：∵x＞0,y＞0,+y²=100,

∴S=xy=x=

∴x²=200,即x=10,S_max=100.

答：花坛的长为10 m，宽为5 m，两喷水器位于矩形分成的两个正方形的中心，就能使花坛的面积最大且能全部喷到水.