题目内容
(本题14分)设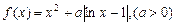
(1)当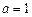 时,求
时,求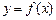 在
在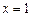 处的切线方程;
处的切线方程;
(2)当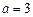 时,求
时,求 的极值;
的极值;
(3)当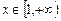 时,求
时,求 的最小值。
的最小值。
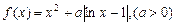
(1)当
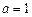 时,求
时,求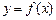 在
在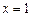 处的切线方程;
处的切线方程;(2)当
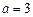 时,求
时,求 的极值;
的极值;(3)当
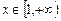 时,求
时,求 的最小值。
的最小值。(1)切线方程为: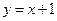
(2) 有极小值
有极小值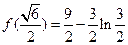
(3)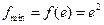
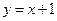
(2)
 有极小值
有极小值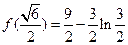
(3)
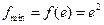
(1)当 时,
时,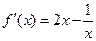 ,∴
,∴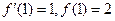 ,
,
∴切线方程为: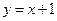 …… 3分
…… 3分
(2)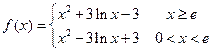
①当 时,
时,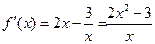 ,
,
故 在
在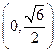 上递减,在
上递减,在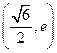 上递增 …… 5分
上递增 …… 5分
②当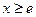 时,
时,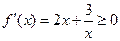 ,故
,故 在
在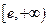 上递增
上递增
∵ 在
在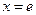 处连续,由①②知,
处连续,由①②知, 在
在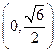 上递减,在
上递减,在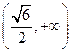 上递增 …… 7分
上递增 …… 7分
故 有极小值
有极小值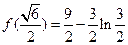 …… 8分
…… 8分
(3)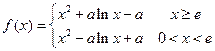
当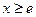 时,
时,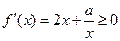 ,故
,故 在
在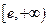 上递增
上递增
当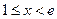 时,
时,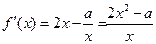
①当 时,
时, 在
在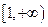 上递增,故
上递增,故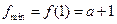 …… 10分
…… 10分
②当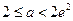 时,
时, 在
在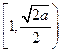 上递减,在
上递减,在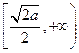 上递增,
上递增,
故 …… 12分
…… 12分
③当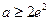 时,
时, 在
在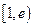 上递减,在
上递减,在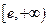 上递增,
上递增,
故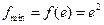 …… 14分
…… 14分
 时,
时,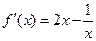 ,∴
,∴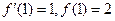 ,
,∴切线方程为:
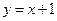 …… 3分
…… 3分(2)
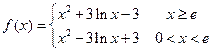
①当
 时,
时,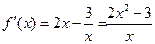 ,
,故
 在
在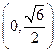 上递减,在
上递减,在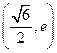 上递增 …… 5分
上递增 …… 5分②当
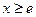 时,
时,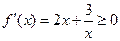 ,故
,故 在
在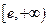 上递增
上递增∵
 在
在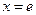 处连续,由①②知,
处连续,由①②知, 在
在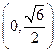 上递减,在
上递减,在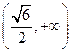 上递增 …… 7分
上递增 …… 7分故
 有极小值
有极小值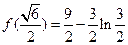 …… 8分
…… 8分(3)
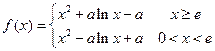
当
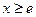 时,
时,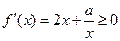 ,故
,故 在
在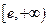 上递增
上递增当
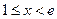 时,
时,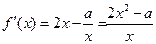
①当
 时,
时, 在
在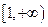 上递增,故
上递增,故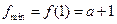 …… 10分
…… 10分②当
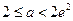 时,
时, 在
在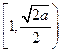 上递减,在
上递减,在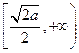 上递增,
上递增,故
 …… 12分
…… 12分③当
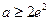 时,
时, 在
在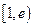 上递减,在
上递减,在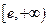 上递增,
上递增,故
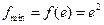 …… 14分
…… 14分
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
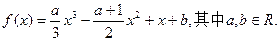
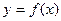 在点
在点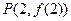 处的切线方程为
处的切线方程为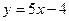 ,求函数
,求函数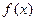 的解析式;
的解析式;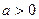 时,讨论函数
时,讨论函数 题满分13分)
题满分13分)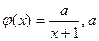 为正常数。
为正常数。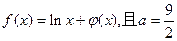 ,求函数
,求函数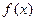
 在区间
在区间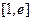 上的最大值与最小值
上的最大值与最小值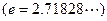 ;
;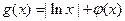 ,且对任意
,且对任意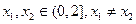 都有
都有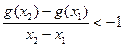 ,求
,求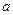 的取值范围。
的取值范围。 题满分 13分)设函数
题满分 13分)设函数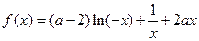 (
(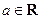 ).
).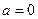 时,求
时,求 的极值;
的极值;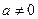 时,求
时,求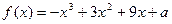 ,若
,若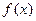 在区间[-2,2]上的最大值为20.
在区间[-2,2]上的最大值为20.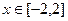 时,
时,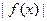 ≤m,(m>0)恒成立.求m的取值范围.
≤m,(m>0)恒成立.求m的取值范围.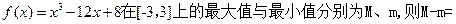 ____.
____.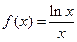 的最大值为 .
的最大值为 .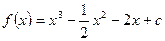 ,若对任意
,若对任意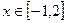 都有
都有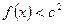 ,则
,则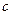 的取值范围是 .
的取值范围是 .