题目内容
(本小 题满分13分)
题满分13分)
已知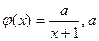 为正常数。
为正常数。
(1)若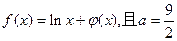 ,求函数
,求函数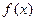
 在区间
在区间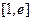 上的最大值与最小值
上的最大值与最小值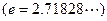 ;
;
(2)若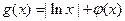 ,且对任意
,且对任意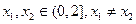 都有
都有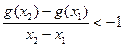 ,求
,求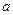 的取值范围。
的取值范围。
 题满分13分)
题满分13分)已知
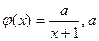 为正常数。
为正常数。(1)若
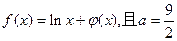 ,求函数
,求函数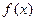
 在区间
在区间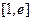 上的最大值与最小值
上的最大值与最小值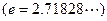 ;
;(2)若
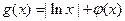 ,且对任意
,且对任意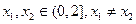 都有
都有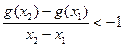 ,求
,求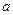 的取值范围。
的取值范围。(1)
(2)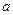 的取值范围是
的取值范围是

(2)
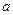 的取值范围是
的取值范围是
解:(1)

 …………(2分)
…………(2分)
故当 时,
时, ,即
,即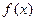 单调递减,从而
单调递减,从而 时,
时,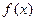 单调递减,
单调递减,
当 时,
时, 单调递增,从而
单调递增,从而 时,
时,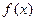 单调递增,…………(
单调递增,…………( 4分)
4分)
故
(2)由
所以可设 ……(8分)
……(8分)
故由题 设可知
设可知 在
在 上为减函数,
上为减函数,
 …………(10分)
…………(10分)
而 由 可得
可得
而 上是增函数,
上是增函数,
显然当
所以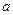 的取值范围是
的取值范围是 ……(13分)
……(13分)


 …………(2分)
…………(2分)故当
 时,
时, ,即
,即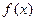 单调递减,从而
单调递减,从而 时,
时,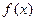 单调递减,
单调递减,当
 时,
时, 单调递增,从而
单调递增,从而 时,
时,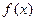 单调递增,…………(
单调递增,…………( 4分)
4分)故

(2)由

所以可设
 ……(8分)
……(8分)故由题
 设可知
设可知 在
在 上为减函数,
上为减函数, …………(10分)
…………(10分)而 由
 可得
可得
而
 上是增函数,
上是增函数,
显然当

所以
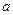 的取值范围是
的取值范围是 ……(13分)
……(13分)
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
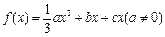 ,已知
,已知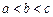 ,且
,且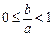 ,曲线
,曲线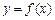 在x=1处取极值.
在x=1处取极值.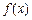 的递增区间为
的递增区间为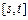 ,求
,求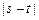 的取值范围; (Ⅱ)如果当
的取值范围; (Ⅱ)如果当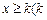 是与
是与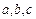 无关的常数
无关的常数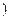 时,恒有
时,恒有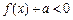 ,求实数
,求实数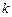 的最小值
的最小值 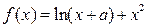
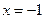 时,
时,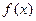 取得极值,求
取得极值,求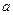 的值,并讨论
的值,并讨论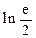 .
.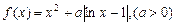
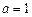 时,求
时,求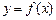 在
在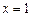 处的切线方程;
处的切线方程;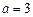 时,求
时,求 的极值;
的极值;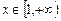 时,求
时,求
 的极值;
的极值; 成立,求实数a的取值范围。
成立,求实数a的取值范围。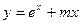 有极值,则实数m的取值范围是
有极值,则实数m的取值范围是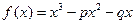 的图象与
的图象与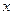 轴切于(1,0)点,则
轴切于(1,0)点,则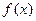 的极值为( )
的极值为( )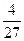 ,极小值为0
,极小值为0
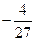
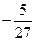 ,极大值为0
,极大值为0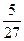
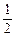
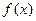 的定义域为区间
的定义域为区间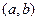 ,导函数
,导函数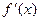 在
在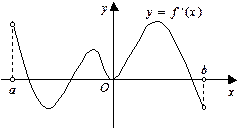
 个
个 个
个 个
个 个[
个[